Aparato y método para calcular operaciones de potenciación y extracción de raíces.

La invención muestra un método y un aparato para el cálculo general de operaciones de potenciación.

El método está basado en la optimización del cálculo XZ=2Zxlog2X. El aparato comprende una pluralidad de elementos de memoria; y un procesador hardware configurado para calcular la operación de potenciación XZ de un número en punto flotante X, donde Z es un exponente sin restricciones. El exponente sin restricciones puede ser un número en punto fijo o punto flotante. Además, el exponente puede ser el inverso de un número lo que permite calcular raíces dentro del mismo procesador aparato. El aparato incluye todos los elementos necesarios para calcular XZ.

Aparato y método para calcular operaciones de potenciación y extracción de raíces

SECTOR TÉCNICO DE LA INVENCIÓN

Las realizaciones mostradas se refieren a aparatos y métodos de computación. Más concretamente, las realizaciones mostradas se refieren a aparatos y métodos para el cálculo de operaciones de potenciación y extracción de raíces.

ESTADO DE LA TÉCNICA

El diseño de unidades funcionales para el cálculo de potencias y raíces q-ésimas (XZ, Z = p o Z = 1/q, donde p y q son enteros) es un reto importante desde hace varios años. Las operaciones de potenciación y de cálculo de raíz q-ésima se emplean con mucha frecuencia en los campos de computación gráfica, procesado digital de señales y cálculos científicos. Estas operaciones incluyen la raíz cuadrada (X1/2) , raíz cuadrada inversa (X-1/2) , raíz cúbica (X1/3) , raíz cúbica inversa (X-1/3) , cuadrado (X2) , cuadrado inverso (X-2) , recíproco (X-1) , exponencial (2y o ey) , y otras operaciones menos frecuentes pero también importantes.

Existen varias arquitecturas para el cálculo de exponenciales y logaritmos; sin embargo el cálculo preciso de operaciones de potenciación y de extracción de raíces en punto flotante es una tarea complicada. Los prohibitivos requerimientos hardware de una implementación basada en tablas y la complejidad intrínseca de los algoritmos basados en la recurrencia de dígitos han provocado que se hayan propuesto soluciones parciales al cómputo de este tipo de operaciones en las que la computación se lleva a cabo para un exponente fijo o para una precisión muy baja. La aproximación tradicional para las operaciones de potenciación o cálculo de raíz qésima ha sido el desarrollo de unidades funcionales para la computación de un exponente o raíz particular. Así, hay un gran número de algoritmos e implementaciones para los exponentes más frecuentes tales como recíprocos, raíz cuadrada o inverso de raíz cuadrada, que incluyen algoritmos de recurrencia de dígitos de convergencia lineal y métodos de convergencia cuadrática basados en multiplicación, tales como los algoritmos de Newton-Raphson y Goldschmidt. También existen varias aproximaciones para el cálculo de otros exponentes derivados de la aplicación de métodos generales para la evaluación de potencias.

En general, el cálculo de una potencia o raíz q-ésima con una precisión muy baja se puede llevar a cabo utilizando una tabla, pero los elevados requerimientos de memoria hacen que esta aproximación sea muy ineficiente para un número en punto flotante con precisión simple o doble. Las aproximaciones racionales y polinómicas representan otra aproximación para el cálculo de potencias y raíces q-ésimas. Sin embargo, uno de los métodos más eficientes para el cálculo de estas operaciones con números en punto flotante son los algoritmos dirigidos por tabla, que están a medio camino entre los las aproximaciones basadas en tablas y las basadas en aproximaciones racionales y polinómicas.

Existen aproximaciones polinómicas de primer y segundo orden basadas en expansiones de Taylor para el cálculo de un número limitado de potencias y raíces, entre ellas raíz cuadrada, recíproco de raíz cuadrada, potencia cuarta, etc., tal y como se describe en Powering by a Table Look-Up and a Multiplication with Operand Modificaction, N. Tagaki, IEEE Transactions on Computers, vol. 47, no. 11, pp. 1216-1222, Nov. 1998; Faithful Powering Computation using Table Lookup and Fused Accumulation Tree, J.A. Piñero, J.D. Bruguera and J.M. Muller, Proceedings 15th IEEE Symposium on Computer Arithmetic, pp. 40-47, Jun- 2001; y High Performance architectures for elementar y function generation, J. Cao, B.W.Y. Wei y J. Cheng, Proceedings 15th IEEE Symposium on Computer Arithmetic, pp. 136-144, Jun. 2001, pero estas implementaciones requieren replicar la tabla de almacenamiento de los coeficientes y no se pueden considerar como unidades de cálculo de raíces qésimas.

Un método de recurrencia de dígitos para el cálculo de la raíz q-ésima se presentó en An Digit-by-Digit Algorithm for m-th Root Extraction, P. Montuchi, J.D. Bruguera, L. Ciminiera y J.A. Piñeiro, IEEE Transactions on Computers, vol.56, no. 12, pp. 1696-1706, Dec. 2007, y particularizado para el cálculo en radix 2 de raíces cúbicas en A Radix-2 Digit-by-Digit Architecture for Cube Root, J.A. Piñeiro, J.D. Bruguera, F. Lamberti, P. Montuschi, IEEE Transactions on Computers, vol. 57, no.4, pp. 562-566., Apr. 2008. La complejidad de las arquitecturas depende de q, con lo que para valores mayores de q hay una mayor complejidad. En consecuencia, una arquitectura para la computación de valores elevados de q en operaciones de raíz q-ésimas es muy compleja. También existen otras implementaciones de métodos de recurrencia de dígitos para el cálculo de raíces cuadradas y cúbicas presentado en Digit-byDigit Methods for Computing Certain Functions, M.D. Ergovac, 41st Asilomar Conference on Signals, Systems and Computers, pp. 338-342, Nov. 2007; y A Digit-Recurrence Algorithm for Cube Rooting, N. Tagaki, IEICE Transactions on Fundamental of Electronics, Communications and Computer Sciences, vol. E84-A, no 5, pp. 1309-1314, May 2001.

Se debe resaltar el hecho de que todos los métodos indicados hasta ahora para el cálculo de una potencia o de una raíz q-ésima están orientados a realizar el cálculo para un exponente fijo. Esto implica que la arquitectura resultante no se puede emplear para calcular potencias o raíces distintas de aquella para la que ha sido diseñada. Para adaptar la arquitectura a una potencia o raíz diferente hay que realizar cambios en las, del inglés Look-up Table (LUT) , en el caso de aproximaciones polinómicas basadas en tabla, o diseñar una nueva arquitectura, en el caso de métodos de recurrencia de dígitos. Las aproximaciones polinómicas basadas en tabla se pueden adaptar para calcular más de una potencia o raíz, pero esto requiere replicar las tablas. De todos modos, los métodos indicados no se puede considerar que sean métodos generales para el calculo de potencias o raíces q-ésimas.

La única arquitectura encontrada en el estado de la técnica para el cálculo de raíces q-ésimas para cualquier q se describe en Algorithm and architecture for Logarithm, Exponential and Powering Computation, J.A. Piñeiro,

M.D. Ergovac and J.D. Bruguera, IEEE Transactions on Computers, vol. 53, no. 9, pp. 1085-1096, Sep. 2004, y fue diseñada para el cálculo de potencias Xp, con p entero, basado en una cadena logaritmo-multiplicaciónexponencial acelerada por el uso de redundancia y aritmética on-line, y extendidas para el cálculo de X1/q. Sin embargo, la implementación de la arquitectura extendida para la raíz q-ésima es muy compleja, porque además de las operaciones en cadena, se incluye una división entera ya que se requiere el cálculo del resto de la división.

DESCRIPCIÓN DE LA INVENCIÓN

Las realizaciones mostradas incluyen un aparato para el cálculo general de operaciones de potenciación y extracción de raíces que comprende (a) una pluralidad de elementos de memoria; y (b) un procesador hardware configurado para calcular la operación de potenciación XZ de un número en punto flotante X, donde Z es un exponente sin restricciones. El exponente sin restricciones puede ser un número en punto fijo o punto flotante. Además, el exponente puede ser el inverso de un número para calcular raíces q-ésimas dentro del mismo procesador hardware. De acuerdo a una realización, el procesador hardware comprende una unidad multiplexora, una unidad recíproca, una unidad logarítmica, una unidad exponencial, una unidad de multiplicación, una unidad de desplazamiento, o una combinación de todas ellas. La unidad recíproca, unidad logarítmica y la unidad de multiplicación están configuradas para llevar a cabo los cálculos concurrentemente, y la unidad exponencial está configurada para llevar a cabo los cálculos de forma on-line. En una realización particular, y sin limitación, las unidades recíproca, logarítmica y de multiplicación están configuradas para realizar los cálculos comenzando por el dígito más significativo. Las realizaciones mostradas también incluyen métodos para calcular funciones de potenciación y extracción de raíces generales.

BREVE DESCRIPCIÓN DE LAS FIGURAS

Las modalidades detalladas en las figuras se ilustran a modo de ejemplo y no a modo de limitación:

La Figura 1 es una secuencia de operaciones para calcular la función de potenciación XZ, con un exponente Z en punto fijo de acuerdo a una realización.

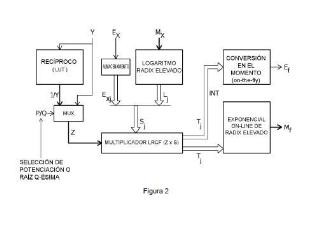
La Figura 2 es un diagrama de bloques de un procesador para calcular la función de potenciación XZ, con un exponente Z en punto fijo de acuerdo a una...

1. Un aparato para el calculo general de potencias y raíces que comprende:

a. una pluralidad de elementos de memoria; y

b. un procesador hardware configurado para calcular la función de potenciación XZ de un número en punto flotante X, donde Z es un exponente sin restricciones.

2. El aparato según la reivindicación 1, aparato (a) , en el que la pluralidad de elementos de memoria almacenan, un número X cuya potencia Z o raíz Z-ésima calcula el aparato, un número en punto fijo Z o punto flotante que indica el exponente de la potencia o raíz que se va a calcular, el número de bits significativos del número X y del resultado del cálculo, la operación llevada a cabo, cálculo de potencia Z o de raíz Z-ésima y el exponente Z.

3. El aparato según reivindicación 1, apartado (b) , donde el exponente sin restricciones es un exponente en punto fijo o punto flotante.

4. El aparato según la reivindicación 3 en el que el exponente sin restricciones es el inverso de un número para calcular el inverso del número y habilitar el cálculo de la raíz q-ésima dentro del mismo procesador hardware.

5. El aparato según la reivindicación 1, aparatado (b) , en el que el procesador hardware comprende:

a. una unidad de cálculo de recíproco que calcula el recíproco de Z obteniendo un número A;

b. una unidad logarítmica que calcula el logaritmo en base 2 del número X resultando en un número B;

c. una unidad de desplazamiento que desplaza el número B en caso de que Z sea un número en punto flotante, cuyo resultado es un número B';

d. una unidad de multiplicación que calcula el producto de los número A y B o B’ resultando en un número C; y

e. una unidad exponencial que calcula la exponencial del número C, obteniendo así el resultado de la operación.

6. El aparato según la reivindicación 5, en el que la unidad de cálculo del recíproco, la unidad logarítmica y la unidad de multiplicación están configuradas para realizar las operaciones concurrentemente.

7. El aparato según la reivindicación 5, apartado (e) , en el que la unidad exponencial está configurada para llevar a cabo las operaciones en forma on-line.

8. El aparato según la reivindicación 5 en el que la unidad recíproca, la unidad logarítmica y la unidad de multiplicación está configuradas para llevar a cabo los cálculos comenzando por el dígito más significativo.

9. El aparato según la reivindicación 1, apartado (b) , en el que el procesador hardware se elige de entre el grupo circuito integrado, dispositivo FPGA, microprocesador, microcontrolador, procesador digital de señal (DSP) , unidad de procesamiento gráfico (GPU) y procesador de propósito general.

10. El aparato según la reivindicación 1 en el que el número X se representa en precisión flotante doble o simple de acuerdo al estándar IEEE-754.

11. Un método de cálculo de la potencia Z-ésima o de la raíz Z-ésima de un número X en un procesador hardware que comprende:

a. almacenar un número X en un primer elemento de memoria del procesador, donde X es un número cuya potencia Z-ésima o raíz Z-ésima se va a calcular;

b. almacenar el número Z en un segundo elemento de memoria del procesador, donde Z es un número de punto fijo o punto flotante que indica el exponente de la potenciación o de la operación de extracción de raíz;

c. almacenar el número de bits significativos del número X y del resultado del cálculo en un tercer 5 elemento de memoria del procesador;

d. almacenar la operación que se va a llevar a cabo, potenciación o raíz, en un cuarto elemento de memoria del procesador;

e. almacenar el exponente del número Z en un quinto elemento de memoria;

f. calcular el recíproco del número Z cuyo resultado es un número A; 10 g. calcular el logaritmo en base 2 del número X cuyo resultado es un número B;

h. desplazar el número B, en caso de que Z sea un número en punto flotante, cuyo resultado es un número B';

i. calcular el producto de los número A y B o B' cuyo resultado es un número C; y

j. separar la parte entera y fraccionaria del número C; y 15 k. calcular la exponencial del número C, que es el resultado final de la operación XZ.

12. EL método según la reivindicación 11 en el que el cálculo de la exponencial y del producto se solapan.

13. El método según la reivindicación 11 en el que el cálculo del producto y el logaritmo se solapan.

14. El método según la reivindicación 11 en el que el número X se representa en precisión flotante doble o simple de acuerdo al estándar IEEE-754.

15. El método según la reivindicación 11 en el que el procesador se escoge de entre el grupo consistente en circuitos integrados, dispositivo FPGA, microprocesador, microcontrolador procesador digital de señal (DSP) , unidad de procesamiento gráfico (GPU) y procesador de propósito general.

Figura 2

OFICINA ESPANOLA DE PATENTES Y MARCAS ESPANA

INFORME SOBRE EL ESTADO DE LA TECNICA

51 Int. Cl. : G06F17/10 (2006.01)

N.O solicitud: 201231286 22 Fecha de presentación de la solicitud: 09.08.2012 32 Fecha de prioridad:

DOCUMENTOS RELEVANTES

Categoría 56 Documentos citados Reivindicaciones afectadas

x VAZQUEZ, A.; BRUGUERA, J.D., "Composite Iterative Algorithm and Architecture for q-th Root 1-15

Calculation, " Computer Arithmetic (ARITH) , 2011 20th IEEE Symposium on, pp.52-61.

2. 27 Julio

2011. doi: 10.1109/ARITH.2011.16

URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5992108&isnumber=5992089

A PINEIRO, J. A.; ERCEGOVAC, M.D.; BRUGUERA, J.D., "Algorithm and architecture for logarithm, 1-15

exponential, and powering computation, " Computers, IEEE Transactions on, vol. 53, no. 9,

pp. 1085-1096, Sept. 2004. doi: 10.1109/TC.2004.53

URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1315603&isnumber=29154

Categoria de los documentos citados x: de particular relevancia Y: de particular relevancia combinado con otro/s de la misma categoria A: refleja el estado de la tecnica O: referido a divulgación no escrita P: publicado entre la fecha de prioridad y la de presentación de la solicitud E: documento anterior, pero publicado despues de la fecha de presentación de la solicitud

El presente informe ha sido realizado • para todas las reivindicaciones • para las reivindicaciones nO:

Fecha de realización del informe 31.01.2013 Examinador M. L. Alvarez Moreno Página 1/4

INFORME DEL ESTADO DE LA TºCNICA

NO de solicitud: 201231286

Documentación minima buscada (sistema de clasificación seguido de los simbolos de clasificación) G06F Bases de datoselectrónicas consultadas durante la bºsqueda (nombre de la base de datos y, si es posible, terminos de

bºsqueda utilizados) INVENES, EPODOC, ºPI, Inspec, Internet

Informe del Estado de la Tecnica Pagina 2/4

OPINIÓN ESCRITA

NO de solicitud: 201231286

Fecha de Realización de la Opinión Escrita: 31.01.2013

Declaración

Novedad (Art. 6.1 LP 11/1986) Reivindicaciones 11-15 Reivindicaciones 1-10 SI NO

Actividad inventiva (Art. 8.1 LP11/1986) Reivindicaciones Reivindicaciones 1-15 SI NO

Se considera que la solicitud cumple con el requisito de aplicación industrial. Este requisito fue evaluado durante la fase de examen formal y tecnico de la solicitud (Articulo 31.2 Ley 11/1986) .

Base de la Opinión.

La presente opinión se ha realizado sobre la base de la solicitud de patente tal y como se publica.

Informe del Estado de la Tecnica Pagina 3/4

OPINIÓN ESCRITA

NO de solicitud: 201231286

1. Documentos considerados.

A continuación se relacionan los documentos pertenecientes al estado de la tecnica tomados en consideración para la realización de esta opinión.

Documento Número Publicación o Identificación Fecha Publicación

D01 VAZQUEZ, A.; BRUGUERA, J.D., "Composite Iterative Algorithm and Architecture for q-th Root Calculation, " Computer Arithmetic (ARITH) , 2011 20th IEEE Symposium on, pp.

5. 61.

2. 27 Julio 2011. doi: 10.1109/ARITH.2011.16 URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=5992108&isnumber=5992089

D02 PINEIRO, J. A.; ERCEGOVAC, M.D.; BRUGUERA, J.D., "Algorithm and architecture for logarithm, exponential, and powering computation, " Computers, IEEE Transactions on, vol. 53, no. 9, pp. 1085-1096, Sept. 2004. doi: 10.1109/TC.2004.53 URL: http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=1315603&isnumber=29154

2. Declaración motivada según los artículos 29.6 y 29.7 del Reglamento de ejecución de la Ley 11/1986, de 20 de marzo, de Patentes sobre la novedad y la actividad inventiva; citas y explicaciones en apoyo de esta declaración Reivindicación independiente 1

La reivindicación caracteriza el aparato por comprender elementos muy generales propios de toda arquitectura implementada en ordenador (elementos de memoria y procesador) , sin definir caracteristicas particulares de los mismos propias de la invención. El documento D01 muestra [Abstract; 1. Introduction] un algoritmo de calculo de raices que permite realizar dicho calculo mediante medios de procesamiento informaticos. Dichosmedios de procesamiento disponen de los elementos de memoria pertinentes (p. ej. diversos registros en todas las figuras) . A la vista del documento D01 la reivindicación 1 carece de novedad segºn el articulo 6 de la Ley de Patentes.

Reivindicación dependientes 2 a 4

Las reivindicaciones 2 a 4 no muestran caracteristicas particulares del aparato, ºnicamente definen el mismo por su capacidad de almacenar información (x, Z...) y operar en punto fijo o flotante. El documento D01 muestra que los requisitos hardware se han optimizado [Abstract] para trabajar en precisión flotante simple o doble. A la vista del documento D01 las reivindicaciones 2 a 4 carecen de novedad segºn el articulo 6 de la Ley de Patentes.

Reivindicaciones dependientes 5 a 10

La arquitectura mostrada en el documento D01 esta formada [figuras 2 y 7] por una unidad de calculo de reciproco, una unidad logaritmica, una uni dad de multiplicación, una u nidad de des plazamiento y una unidad e xponencial on -line. E l documento indica [pagina 6] que el calculo de la extracción de raiz se realiza mediante una secuencia de operaciones, las cuales pueden realizarse de forma concurrente, comenzando los calculos por el digito mas significativo. Al igual que en D01, los requisitos hardware se han optimizado [Abstract] para trabajar en precisión flotante simple o doble. Puede verse que el documento D01 contiene todas las caracteristicas definidas en las reivindicaciones 5 a 8 y 10. La reivindicación 9 no define caracteristicas particulares del procesador, pudiendo utilizarse cualquiera de los habitualmente utilizados para este tipo de calculos. A la vista del D01 las reivindicaciones 5 a 10 carecen de novedad segºn el articulo 6 de la Ley de Patentes.

Reivindicación independiente 11

El doc umento D 01 m uestra e xplicitamente [ pagina 7; figura 1] ci ertas etapas coincidentes con l as definidas en l a reivindicación 11. Estas etapas explicitamente citadas son: calculo del reciproco del nºmero Z (exponente) , calculo del logaritmo en base 2 de x, calcular el producto de los resultados anteriores, separar la parte entera y fraccionaria del resultado anterior y calcular el exponente del mismo. En casos particulares [pagina 15; figura 6] tambien se realiza un desplazamiento del l ogaritmo previamente c alculado e n l a et apa g. E l documento D 01 no m uestra de f orma e xpresa l as acciones de almacenamiento, en elementos de memoria, de la información imprescindible para realizar el calculo (x, Z, nºmero de bits significativos...) , pero de la lectura del documento se pueden deducir dichas acciones ya que son los valores que algoritmo considera como punto de partida [Tabla 1] para su posterior procesamiento. A la vista del documento D01 la reivindicación 11 carece de actividad inventiva segºn el articulo 8 de la Ley de Patentes.

Reivindicaciones dependientes 12 a 15

El documento D01 indica [pagina 6] que el calculo de la extracción de raiz se realiza mediante una secuencia de operaciones, las cuales pueden realizarse de forma concurrente. Los requisitos hardware se han optimizado [Abstract] para trabajar en precisión flotante simple o doble. Puede verse que el documento D01 identifica todas las caracteristicas definidas en las reivindicaciones 12 a 14. La reivindicación 15 no define ninguna etapa del procedimiento, pudiendo utilizarse cualquiera d e l os procesadores habitualmente ut ilizados para est e t ipo de ca lculos. A l a vi sta del docu mento D 01 l as reivindicaciones 12 a 15 carecen de actividad inventiva segºn el articulo 8 de la Ley de Patentes.

Informe del Estado de la Tecnica Pagina 4/4