METODO Y SISTEMA PARA ANALISIS DE SINGULARIDADES EN SEÑALES DIGITALES.
Método y sistema para análisis de singularidades en señales digitales.
El método propuesto comprende determinar para cada punto de la señal un entorno que comprende los primeros vecinos y calcular para cada punto de la señal una medida de reconstructibilidad, o medida de singularidad, ponderando las contribuciones de dicho entorno local del punto. El valor de la señal en cada punto se infiere a partir de los valores de la señal en los puntos del entorno local utilizando una fórmula de reconstrucción. La medida de singularidad incluye la diferencia entre el valor de la señal en el punto y el valor estimado por su entorno local. Sobre dicha medida de singularidad se realiza una transformación logarítmica con el fin de obtener una medida independiente de la amplitud de la señal digital muestreada y que varíe de una manera controlada bajo cambios de resolución.
Se propone un sistema con medios para obtener para cada punto dicha medida de singularidad y para realizar la referida transformación logarítmica y otros cálculos
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P200702829.
Solicitante: CONSEJO SUPERIOR DE INVESTIGACIONES CIENTIFICAS.
Nacionalidad solicitante: España.
Provincia: MADRID.
Inventor/es: TURIEL MARTINEZ,ANTONIO MARIA.
Fecha de Solicitud: 26 de Octubre de 2007.
Fecha de Publicación: .
Fecha de Concesión: 11 de Marzo de 2010.
Clasificación Internacional de Patentes:
- G06K9/46R
- G06K9/52W
- G06T5/00E
- G06T9/00V
Clasificación PCT:
- G06K9/46 FISICA. › G06 CALCULO; CONTEO. › G06K RECONOCIMIENTO DE DATOS; PRESENTACION DE DATOS; SOPORTES DE REGISTROS; MANIPULACION DE SOPORTES DE REGISTROS (impresión per se B41J). › G06K 9/00 Métodos o disposiciones para la lectura o el reconocimiento de caracteres impresos o escritos o el reconocimiento de formas, p. ej. de huellas dactilares (métodos y disposiciones para la lectura de grafos o para la conversión de patrones de parámetros mecánicos, p.e. la fuerza o la presencia, en señales eléctricas G06K 11/00; reconocimiento de la voz G10L 15/00). › Extracción de elementos o de características de la imagen.
- G06K9/52 G06K 9/00 […] › deduciendo las propiedades matemáticas o geométricas de la imagen completa.
- G06T5/00 G06 […] › G06T TRATAMIENTO O GENERACIÓN DE DATOS DE IMAGEN, EN GENERAL. › Perfeccionamiento o restauración de imagen.
- G06T9/00 G06T […] › Codificación de imagen, (reducción del ancho de banda o de la redundancia para imagenes estáticas H04N 1/41; codificación o descodificación de señales de imagenes de color estáticas H04N 1/64; métodos o disposiciones para la codificación, descodificación, compresión o descompresión de señales de video digital H04N 19/00).
Fragmento de la descripción:
Método y sistema para análisis de singularidades en señales digitales.
Campo de la invención
La presente invención concierne al análisis de señales digitales, es decir señales que están muestreadas a intervalos regulares, aplicando para la puesta en práctica del método propuesto análisis de wavelets (ondículas o pequeñas ondas) que permite identificar algunos subconjuntos de puntos particulares en el espacio a una escala y posición que son más informativos acerca de la señal que otros.
La invención hace referencia igualmente a un sistema para la implementación del método propuesto.
En esta memoria descriptiva se entenderá como señal digital cualquier colección estructurada de datos muestreada uniformemente que se pueda representar mediante una matriz multidimensional cuyas posiciones se denominan puntos de la señal.
La invención aporta técnicas y herramientas útiles para el procesado, reconstrucción y compresión de señales digitales a partir de información parcial acerca de su gradiente y en particular operando sobre la base de medidas basadas en gradientes obtenidos por incrementos finitos. Dichas técnicas y herramientas son implementables de manera ventajosa mediante algoritmos automáticos materializados en programas de ordenador ejecutables en entornos computacionales.
La invención, dada la gran eficiencia que proporciona principalmente en tareas de reconstrucción de señales digitales, en particular representativas de imágenes, encuentra aplicación en numerosos campos entre los cuales cabe citar como aplicaciones específicas la compresión de señales digitales (incluyendo la compresión de imagen) y la evaluación de líneas de flujo en señales referidas a fluidos (incluyendo la determinación de líneas de corriente en imágenes de fenómenos físicos); y como aplicaciones más generales la detección de estructuras y el reconocimiento de patrones en imágenes de entornos reales tales como imágenes fotográficas, geofísicas, biomédicas y de otros tipos.
La invención concierne señales definidas en cualquier número de dimensiones, aunque una vez descrito el método para un número determinado de dimensiones (por ejemplo dos), resultará bastante evidente para un experto en el sector generalizarlas para señales definidas en cualquier número de dimensiones. Por ello, en aras de simplicidad, muchas de las ecuaciones y derivadas presentadas a lo largo de esta memoria descriptiva se han escrito para señales 2D, es decir bidimensionales, susceptibles de constituir elementos tales como imágenes. Sin embargo, también se han obtenido resultados útiles en otros números de dimensiones y en particular en el procesamiento de señales 1D, como las series temporales de la bolsa (ver referencias [16], [17]).
Antecedentes de la invención
Las patentes US-A-5901249, US-A-6141452 y US-A-6865291 se refieren a técnicas de compresión de señales digitales utilizando análisis de wavelets.
La patente US-A-6434261 describe un método para detección y segmentación de imágenes digitales para localizar objetivos en dichas imágenes basado en una determinación de un umbral adaptativo para realizar un análisis de wavelets de las imágenes digitales que son descompuestas en diferentes canales de escala.
La patente US-A-7181056 concierne a un método para la detección automática de regiones de interés en una imagen digital representativa de al menos una porción de un tejido biológico, en donde se genera una representación basada en wavelets de las regiones a explorar.
La patente US-A-7062085 se refiere a un método para detectar aspectos en regiones de imágenes en color en donde se hace referencia a unas características de textura materializadas mediante coeficientes derivados de una transformada wavelet basada en análisis de multiresolución de la imagen digital en color.
La solicitud de patente US-A-2005/0259889 hace referencia a un método para la eliminación de ruido de una imagen radiológica comprendiendo la aplicación de una transformación wavelet compleja a la imagen portadora de un motivo, operando con los coeficientes wavelet para reducir el ruido.
La solicitud de patente WO-A-2004/068410 concierne a un método para la detección de puntos de interés en una imagen digital que implementa una transformación wavelet, asociando una imagen sub-muestreada con una imagen origen.
El análisis de singularidad (ver referencia [14]) que implementa el concepto de caracterizar el comportamiento local de una función f(x) estimada en Rm y definida sobre Rd alrededor de cada uno de sus puntos de dominio x de acuerdo con el denominado exponente de singularidad de Hölder o, exponente Hurst denotado por h(x), es muy útil para muchas tareas de procesado de señales, y en particular, es muy relevante para fines de compresión y como herramienta de reconocimiento de patrones, y, dependiendo del contexto, puede ser utilizado también para revelar información sobre la evolución y dinámica de señales complejas.
La patente US-A-6745129 concierne a un método basado en wavelets para el análisis de singularidades en datos sísmicos a partir del procesado de una serie temporal representativa de un registro del fenómeno. El objeto de esta patente es calcular el exponente de Hölder sobre registros sísmicos a través de una transformada de wavelet continua. Mediante ese método, al realizar el análisis de la señal (según se muestra en la Figura 2b de dicha patente), se producen inestablilidades que repercuten tanto en la resolución espacial como en la calidad de la determinación del exponente de Hölder de cada punto (ver discusión de esta cuestión en la referencia [11]). Esta problemática imposibilita de hecho la utilización del método de la US-A-6745129 para tareas de reconstrucción de señales digitales a diferencia de las propuestas del método de la presente invención. La presente invención proporciona una determinación más precisa de los exponentes de singularidad, tanto en cuanto a su posición, como en cuanto a su valor. La diferencia de precisión entre la presente invención y la US-A-6745129 es debida al uso de medidas de gradiente (que elimina las fluctuaciones indeseables asociadas a las wavelets complejas (ver referencia [17]) y también por incorporar dicha medida un indicador del grado de reconstructibilidad. En base a lo anterior, la presente invención permite además reconstruir una señal con gran calidad a partir de información parcial, al contrario del método de la patente US-A-6745129 (ver referencia [11]).
Dentro del campo del análisis de señales basado en wavelets y en particular aplicado al procesado de señales digitales uno de los métodos utilizados más conocidos es el denominado Máximos del Módulo de la Transformada de Wavelet (conocido como WTMM, por sus siglas en inglés) que está determinado por el máximo local de las proyecciones de wavelet. Mallat y Zhong (ver referencias [4], [5] y [6]) conjeturaron que este conjunto puede ser utilizado para reconstruir de manera completa la señal. Con posterioridad se ha verificado que el conjunto conduce a una señal atenuada y que se han de introducir varios coeficientes empíricos para poder reproducir las amplitudes correctas de la señal. Desde la publicación del documento de Mallat y Zhong ha habido múltiples intentos de obtener reconstrucción de alta calidad a partir de WTMM. En cualquier caso, lo mas interesante acerca del método WTMM es que en el caso de imágenes la mayor cantidad de líneas están concentradas alrededor de los bordes y contornos; y puesto que desde hace años se conoce (ver referencia [7]) que los bordes y contornos contienen la mayoría de la información de una escena visual, el WTMM se ha evidenciado como un buen candidato para extraer información perceptual (bordes) utilizando un algoritmo automático canónico basado en dicho método.
Otra rama de investigación también centrada en el uso del WTMM fue iniciada por Arneodo y colaboradores (ver referencias [1] y [2]) que reconocieron la capacidad de que el WTMM pueda tratar con señales multiescala, centrando sus estudios en sistemas en los que se conocía que presentaban propiedades de invariancia de escala, tales como flujos turbulentos y sistemas caóticos.
El principal inconveniente de todas las propuestas basadas en el WTMM es la imposibilidad de extraer de manera sistemática los máximos cuando éstos se acumulan (topológicamente), situación que ocurre siempre cuando se trata de señales reales, como se discute en [17]. En [10] se estudió el problema y se...
Reivindicaciones:
1. Método para análisis de singularidades en señales digitales, caracterizado porque comprende las siguientes etapas:
a) determinar para cada punto x de la señal un entorno de primeros vecinos o entorno local; y
b) calcular para cada punto x de la señal una medida de reconstructibilidad, o medida de singularidad, a partir del entorno local asociado, construida a partir de la inferencia del valor de la señal en dicho punto a partir del valor de los puntos de dicho entorno local utilizando la siguiente fórmula de reconstrucción
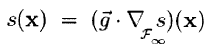
donde:
- s es una señal dada,
- 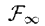 es la variedad más singular o MSM de dicha señal s,
es la variedad más singular o MSM de dicha señal s,
- 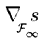 es el gradiente esencial de s,
es el gradiente esencial de s,
-
- el símbolo significa producto escalar de convolución
estando dicha fórmula de reconstrucción adaptada al citado entorno, de manera que la medida de singularidad contiene la diferencia entre el valor medido y el valor inferido por la fórmula de reconstrucción.
2. Método de acuerdo con la reivindicación 1, caracterizado por incluir además una tercera etapa c) que comprende realizar al menos una transformación logarítmica sobre dicha medida de singularidad que suprime la dependencia de la medida del número de puntos de la señal, obteniendo un exponente de singularidad para cada punto de la señal.
3. Método de acuerdo con la reivindicación 2, caracterizado porque comprende, antes de realizar la etapa a), obtener una función derivada estable de dicha señal digital que está muestreada a intervalos regulares, y porque en la etapa b) comprende obtener para cada punto de dicha señal digital muestreada una medida de singularidad de la función en ese punto, ponderando las contribuciones de un entorno local del punto y el valor de la derivada en todos los puntos de dicho entorno local.
4. Método según la reivindicación 3, caracterizado porque la derivada estable de la señal digital que precede a la etapa a) se obtiene por derivada de incrementos de un punto hacia la derecha o incrementos centrados de medio punto, estando en ambos casos la derivada definida en el espacio de Fourier por la multiplicación de la señal por los correspondientes núcleos de derivación, donde asumiendo que hay Nx puntos en una dirección coordenada x en la que se quiere derivar, los núcleos de derivación se expresan como sigue:
Diferencia de un punto hacia la derecha:

Diferencia centrada de medio punto:
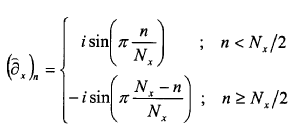
comprendiendo las siguientes etapas:
- se aplica la transformada de Fourier a dicha señal;
- se multiplica por el núcleo asociado a cada una de las d componentes una copia de la transformada de Fourier de la señal; y
- se aplica la antitransformada a estas d componentes.
5. Método de acuerdo con la reivindicación 2, caracterizado porque la transformación logarítmica de la etapa c) que es al menos una, se realiza de la forma siguiente:
6. Método de acuerdo con la reivindicación 5, caracterizado porque la medida de singularidad definida en la etapa b) se calcula mediante los siguientes pasos:
7. Método de acuerdo con la reivindicación 6 caracterizado porque el citado operador de gradiente local aplicado al vector de (2 × d)+1 componentes comprende, para cada entorno de un punto x definido por el vector de (2 × d) +1 componentes que incluye el valor de la señal en el punto x y en sus (2 × d) vecinos, ejecutar una transformada de Fourier local, que sólo tiene en cuenta este entorno.
8. Método de acuerdo con la reivindicación 7, caracterizado porque la citada transformada de Fourier local está construida como una matriz de ((2 × d)+1)) × ((2 × d)+1)), cuyos elementos son todos de valor 1 excepto los de la diagonal principal y de las diagonales adyacentes, donde todos los elementos de la diagonal principal excepto el primero por la izquierda, que vale 1, valen la exponencial compleja 2 × p × i/3 donde i es la raíz cuadrada de -1 y los elementos de las diagonales adyacentes valen consecutivamente 1, exponencial de -2 × p × i/3, 1, y así sucesivamente, comenzando desde arriba a la izquierda hacia abajo a la derecha.
9. Método de acuerdo con la reivindicación 8, caracterizado porque se calcula la transformada de Fourier local, aplicando matricialmente la matriz descrita de ((2 × d)+1)) x ((2 × d)+1)) a un vector de entorno de (2 × d)+1 componentes.
10. Método de acuerdo con la reivindicación 9, caracterizado porque se calcula la antitransformada de Fourier local aplicando la matriz inversa de la descrita en la reivindicación 8, la cual existe siempre.
11. Método de acuerdo con la reivindicación 10 caracterizado porque para cada entorno de un punto x definido por un vector
12. Método de acuerdo con la reivindicación 6 caracterizado porque dicho operador de reconstrucción aplicado al gradiente local se define como el inverso del operador de gradiente local, y comprende las siguientes etapas:
- se aplica la transformada de Fourier local a los d vectores de derivada a lo largo de cada dirección coordenada, cada uno de (2 × d)+1 componentes;
- se construye el vector de reconstrucción a lo largo de una dirección coordenada dada dividiendo por i
13. Método de acuerdo con la reivindicación 6, caracterizado porque el paso final de la etapa b) por el que se obtiene la medida de singularidad asociada al punto x comprende:
con lo que se obtiene una medida de singularidad de correlación local apta para medir la impredecibilidad de un punto dado.
14. Método de acuerdo con la reivindicación 6, caracterizado porque el paso final de la etapa b) por el que se obtiene la medida de singularidad asociada al punto x comprende:
con lo que se obtiene un índice de alineación de diferencias de gradiente que permite deducir la existencia de una coherencia espacial entre los errores cometidos al prescindir del punto central cuando la señal es reconstruida, lo cual permite diferenciar entre ruido (de orientación aleatoria) y señal coherente.
15. Método de acuerdo con la reivindicación 14, caracterizado porque comprende además:
16. Método según la reivindicación 15, caracterizado porque la derivada estable de la señal digital que precede a la etapa a) se obtiene por derivada de incrementos de un punto hacia la derecha o incrementos centrados de medio punto, estando en ambos casos definida la derivada en el espacio de Fourier por la multiplicación de la señal por los correspondientes núcleos de derivación, donde asumiendo que hay Nx puntos en una dirección coordenada x en la que se quiere derivar dichos núcleos de derivación, los núcleos de derivación se expresan como sigue:
Diferencia de un punto hacia la derecha:
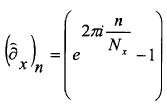
Diferencia centrada de medio punto:
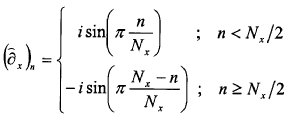
comprendiendo las siguientes etapas:
- se aplica la transformada de Fourier a dicha señal;
- se multiplica por el núcleo asociado a cada una de las d componentes una copia de la transformada de Fourier de la señal; y
- se aplica la antitransformada a estas d componentes
17. Sistema para análisis de singularidades en señales digitales caracterizado por comprender:
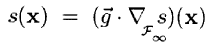
donde:
- s es una señal dada,
- 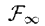 es la variedad más singular o MSM de dicha señal s,
es la variedad más singular o MSM de dicha señal s,
- 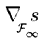 es el gradiente esencial de s,
es el gradiente esencial de s,
-
- el símbolo significa producto escalar de convolución, conteniendo dicha medida de singularidad la diferencia entre el valor medido y el valor inferido para cada punto.
18. Sistema de acuerdo con la reivindicación 17 caracterizado por incluir además medios para realizar al menos una transformación logarítmica sobre dicha medida de reconstructibilidad que suprime la dependencia del número de puntos de la señal, lo que proporciona un exponente de singularidad para cada punto de la señal.
19. Sistema de acuerdo con la reivindicación 18, caracterizado por comprender además:
medios para obtener una función derivada estable de la señal digital, muestreada a intervalos regulares; y
medios para obtener para cada punto de dicha señal digital muestreada una medida de singularidad de la señal en ese punto, ponderando las contribuciones del citado entorno local del punto y el valor de dicha derivada estable en todos los puntos de dicho entorno local.
Patentes similares o relacionadas:
APARATO DE TRANSFORMACIÓN DE HACES PEQUEÑOS ADAPTADOS A UNA CARACTERÍSTICA Y METODOLOGÍA ASOCIADA DE DETECCIÓN DE OBJETOS CURVILÍNEOS DE UNA IMAGEN, del 8 de Febrero de 2012, de INSTITUT PASTEUR GENOMIC VISION: Procedimiento de detección de un objeto curvilíneo de una imagen con ruido (f), que comprende: filtrar la imagen con ruido (f) utilizando un filtro […]
Almacenamiento eficiente de registros de códigos cifrados estructurados múltiples, del 22 de Julio de 2020, de Nokia Technologies OY: Un aparato que comprende: medios para formar un vector de código base combinando componentes 5 de vector de un sub-vector señalado por […]
Método para el movimiento de diente como una bandada, del 24 de Junio de 2020, de ULAB SYSTEMS, INC: Método de control de movimientos de diente para corregir maloclusiones, que comprende: recibir una pluralidad de modelos de diente digitales […]
Procedimiento de codificación de imágenes, procedimiento de descodificación de imágenes, aparato de codificación de imágenes, aparato de descodificación de imágenes y aparato de codificación / descodificación de imágenes, del 27 de Mayo de 2020, de Sun Patent Trust: Un procedimiento de codificación de imágenes que comprende: dividir (S201) una imagen en mosaicos; codificar (S202) los mosaicos para […]
Procedimiento de decodificación de imágenes y aparato de decodificación de imágenes, del 18 de Marzo de 2020, de KABUSHIKI KAISHA TOSHIBA: Un procedimiento de decodificación que comprende: determinar, mediante una unidad de decodificación, un modo de predicción según un modo […]
Método y aparato para representar granularidad de imagen mediante uno o más parámetros, del 26 de Febrero de 2020, de DOLBY INTERNATIONAL AB: Un método para simular grano de película, que comprende: recibir un flujo de vídeo codificado; recibir información codificada de grano de película, […]
Interpolación mejorada de cuadros de compresión de vídeo, del 4 de Diciembre de 2019, de DOLBY LABORATORIES LICENSING CORPORATION: Un método para compresión de imágenes de video usando predicción en modo directo, que incluye: proporcionar una secuencia de cuadros predichos […]
Interpolación mejorada de cuadros de compresión de vídeo, del 4 de Diciembre de 2019, de DOLBY LABORATORIES LICENSING CORPORATION: Un método de compresión de imágenes de video que comprende: proporcionar una secuencia de cuadros referenciables (I, P) y predichos bidireccionales […]