La presente invención se refiere a un método para aplicar en las células de recurrencia de un circuito divisor para dividir un dividendo de coma fija por un divisor de coma fija.

Además se proporcionan dichas células de recurrencia y un circuito divisor, que divide en una base r = 2k, generando k bits en cada iteración. El divisor divide un dividendo X de n bits por un divisor Y de m bits mayor que cero, devolviendo un cociente Q de n bits y un resto R de m bits. La presente invención hace la división más rápida, preferentemente usando una propagación de acarreo eficaz para la suma y la resta. El circuito divisor puede modificarse fácilmente con el fin de devolver más bits fraccionales en el cociente Q. Se describen dos arquitecturas, denominadas para la célula de recurrencia de dígitos. La primera es para una implementación de hardware general y la segunda está optimizada para la lógica programable. También se proporciona un conjunto de instrucciones para implementar dicho método en un medio programable, y/o configurar dicho u otro medio programable.

Método, célula de recurrencia y circuito para realizar divisiones con operandos de coma fija de alta velocidad.

Campo de la invención

La presente invención se encuentra dentro del campo de las divisiones entre dos números de coma fija. Más en particular, se refiere a un método para aplicar en una célula de recurrencia de un circuito divisor, dicha célula de recurrencia y un circuito divisor que comprende estas células. La invención puede adaptarse para llevar a cabo la división entre un dividendo con signo y un divisor con signo, y además, obtener dígitos fraccionales adicionales en el resultado.

Antecedentes de la invención

La división digital de dos valores binarios ha sido implementada de varias maneras. Puede encontrar descripciones completas en la bibliografía (1) J.P. Deschamps, G.A. Bioul, and G. Sutter, "Synthesis of Arithmetic Circuits: FPGA, ASIC and Embedded Systems", Wiley Intescience. 2006. (2) S.F. Oberman and M.J. Flynn. "Division algorithms and implementations". IEEE Transactions on Computers. 46(8):833-854. August 1997. (3) B. Parhami. Computer Arithmetic: Algorithms and Hardware Design. Oxford University Press. 2000. (4) Milos. D. Ercegovac and Tomas Lang. Digital arithmetic San Francisco. California: Morgan Kaufmann. cop. 2004.

A modo de resumen, cuando los operandos están normalizados pueden aplicarse varios algoritmos de recurrencia como el SRT (Sweeney-Robertson-Tocher) en diferentes bases y representaciones del resto, ó bien con algoritmos de convergencia de dígitos como Newton-Rapshon, Goldschmidt (Expansión de MacLaurin), etc. Si los operandos no están normalizados se aplican normalmente los algoritmos binarios de división con restauración y sin restauración. Aunque pueden utilizarse bases superiores normalmente con el fin de hacer más rápidos estos algoritmos, las implementaciones de la división con lógica programable más comunes (Xilinx y Altera) utilizan algoritmos de división sin restauración en base 2.

Los costes de área C y de tiempo T de los circuitos divisores de base 2 para un dividendo X de n bits y un divisor Y de m bits que retorna un cociente Q de n bits y un resto R de m bits son distintos para la división con restauración y sin restauración, dependiendo de los siguientes parámetros:

- el coste de área de un restador de m+1 bits, C_restador(m+1);

- el coste de área de un sumador-restador de m+1 bits, C_{sumador-restador}(m+1);

- el coste de área de un sumador de m bits, C_sumador(m);

- el coste de área de un multiplexador de 2 a 1, C_mux;

- el retardo de un restador de m+1 bits, T_restador(m+1);

- el retardo de un sumador-restador de m+1 bits, T_{sumador-restador}(m+1);

- el retardo de un sumador de m bits, T_sumador(m); y

- el retardo de un multiplexador de 2 a 1, T_mux.

Así para la división con restauración el coste de área y el de tiempo quedan:

- C(n,m) = n×(C_restador(m+1) + m×C_mux), y

- T(n,m) = n×(T_restador(m+1) + T_mux).

Mientras que para la división sin restauración, quedan como

- C(n,m) = n×C_{sumador-restador}(m+1) + C_mux + C_sumador (m), y

- T(n,m)=n×T_{sumador-restador}(m+1) + T_sumador(m).

Dichos componentes constituyen una unidad capaz de realizar un conjunto de operaciones aritméticas sobre un conjunto de números expresados en una base r=2^k que se denomina célula_base_2^k. El resultado del conjunto de operaciones de la célula_base_2^k comprende un cociente de k dígitos y un nuevo resto de m+1 dígitos.

Si se utilizan bases mayores con el fin de acelerar el proceso de división. El área y el tiempo esperados para una base r = 2^k son:

C(n,m,k) = (n/k) C_{célula_base2^wedge k}(m) + C_mux + C_sumador (m), y

T(n,m,k) = (n/k)T_{célula_base2^wedge k}(m) + T_sumador(m).

Los esfuerzos en acelerar el cómputo se basan en utilizar métodos de división y células con el menor retardo posible y con un coste en área menor e implementar mediante ellos un circuito divisor.

Resumen de la invención

El objeto de la invención es proporcionar un método más rápido y con menor costo de área para hallar los restos parciales y los cocientes durante las etapas de una división sin restauración en una célula de base 2^k según la reivindicación 1 independiente. Además, en un segundo aspecto se proporciona una célula de base 2^k según la reivindicación independiente 4. En un tercer aspecto se proporciona un circuito divisor según una primera arquitectura en la reivindicación 11 independiente, y en un cuarto aspecto inventivo se reivindica un circuito divisor según una segunda arquitectura en la reivindicación 14. Conjuntamente se proporciona en un quinto aspecto un conjunto de instrucciones que pueden ejecutarse en un medio programable que llevan a cabo las variantes de realización definidas por cualquiera de los aspectos inventivos segundo, tercero o cuarto. Además, en un sexto aspecto inventivo se proporciona un producto destinado a ejecutarse en medios programables que c comprende un conjunto de instrucciones según la reivindicación 19.

En una división sin restauración en base 2^k de un dividendo de n dígitos entre un divisor de m dígitos comprende p=0, .., [n/k] pasos en los que se halla en cada etapa:

• un resto parcial R(p) de m+1 dígitos;

• un conjunto de k dígitos del cociente q(k+p), ..., q(p).

En un primer aspecto inventivo se describe un método para aplicar a una célula célula_base_2^k en que calcula en paralelo de todos los posibles restos en base y de las condiciones de selección del resto correcto.

En una primera etapa se le suministran a cada célula:

- un registro rem(m...0) correspondiente al resto parcial R(p) de los p=0, .., [n/k] de los restos parciales;

- 2^k-1 registros Reg_(2j-1)Y de m+j dígitos, j= 0, .., 2^k-1 que contienen los múltiplos impares del divisor Y (Y, 3Y, ... (2^k-1)Y);

- Un registro sX(k-1...0) de k dígitos del dividendo X. Estos dígitos son en cada ciclo p el registro sX(k-1...0) ≤ftarrow X(n-k×p, ... n-k×(p+1)). que se corresponde con los k bits más significativos desplazados en cada ciclo a la izquierda p veces.

En una segunda etapa se calculan los valores posibles de la suma y de la resta de los 2^k-1 múltiplos impares del divisor con el valor del resto parcial.

En una tercera etapa se determina a su vez, de entre estos posibles valores de los restos, el valor del resto parcial siguiente R(p+1) a partir de los signos de estos valores posibles del resto como c(k-1) rightarrow R(p+1). Utilizando la siguiente secuencia:

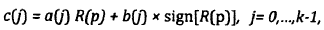
dónde

a(0) = 2;

b(0) = 1;

a(j+1) = 2×a(j)

b(j+1) = 2×b(j) + 1 si c(j) < 0

ó

b(j+1) = 2×b(j) - 1 si c(j) > 0

En una cuarta etapa, los signos de los valores posibles del resto son utilizados para calcular los k dígitos del cociente q(k+p), ..., q(p) asignándose el valor... [Seguir leyendo]

1. Método para hallar los restos durante una división sin restauración en una célula de base 2^k entre un dividendo X de n bits y un divisor Y de m bits que en la etapa p (p=0...[n/k]) de la división sin restauración comprende las siguientes etapas:

a. se introducen 2^k-1 registros correspondientes a múltiplos impares del divisor Y, el registro sX de k dígitos correspondientes al dividendo X, y el registro de resto parcial R(p),

b. se hallan los diferentes posibles valores del resto calculando los posibles restos parciales mediante las sumas y/o restas,

c. se selecciona el resto parcial R(p+1) que coincide con la secuencia que determina el conjunto de restos c(j), j=0, ..., k-1 en función de los signos de c(j) y permite determinar el siguiente resto parcial R(p+1)= c(k-1), utilizando la siguiente secuencia:

d. se utilizan los signos de la secuencia de restos parciales c(0), ..., c(k-1) para determinar los k nuevos dígitos del cociente q(k-1)...q(0),

de tal manera que se proporciona un registro new_q(k-1...0) que contiene k dígitos del cociente Q y un registro new_rem del resto parcial.

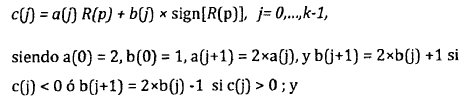
2. Método según la reivindicación 1 caracterizado porque la representación de los números es binaria de complemento a dos.

3. Método según la reivindicación 2 caracterizado porque los bits del signo de cada uno de los números del conjunto de restos c(j) se concatenan para obtener los bits del cociente.

4. Célula para hallar k dígitos de un cociente Q y un valor de un resto parcial R(p+1) entre un dividendo X de n bits y un divisor Y de m bits que comprende:

a. medios adaptados para introducir registros de memoria y para proporcionar registros de memoria,

b. medios adaptados para realizar operaciones aritméticas,

c. medios adaptados para realizar operaciones lógicas, y

d. medios adaptados para interconectar al menos estos componentes,

configurados para implementar el método según la reivindicación 1 a 3.

5. Célula según la reivindicación anterior caracterizada porque los medios adaptados para realizar las operaciones lógicas son multiplexores.

6. Célula según la reivindicación anterior caracterizada porque comprende 1+2^k-1 multiplexores para implementar la selección del resto parcial en función del bit de los posibles restos parciales y un multiplexor para seleccionar el registro del cociente.

7. Célula según cualquiera de las reivindicaciones 4 a 6 caracterizada porque comprende sumadores condicionales que determina la operación suma o resta entre dos posibles valores de restos correspondientes a c(j), j=1, ..., k-1 en función del bit más significativo del registro del resto parcial c(j-1).

8. Célula según la reivindicación caracterizada porque los dígitos q(k-1-j), j=0, ..., k-1 del registro del cociente q(k-1-j) corresponden a la concatenación de los bits de signo de los restos parciales según el bit más significativo del registro del resto c(j) con una representación binaria de complemento a dos.

9. Célula según la reivindicación 2 caracterizada porque está implementada utilizando una arquitectura en donde los multiplexores seleccionan los registros de los restos c(j), j= 0, ..., k-1.

10. Célula según la reivindicación 2 caracterizada porque está implementada utilizando una arquitectura en donde los sumadores condicionales seleccionan los registros de los restos c(j), j= 0, ..., k-1.

11. Circuito para implementar un método de división sin restauración que comprende una célula de base 2^k en la que se introducen los múltiplos impares del divisor, el resto parcial y k bits del dividendo y genera como resultado k bits de cociente y un nuevo resto para la siguiente etapa en donde la arquitectura es secuencial.

12. Circuito según la reivindicación anterior caracterizado porque comprende:

- una célula de base 2^k según cualquiera de las reivindicaciones 3 a 7

- un medio de control que proporciona y recibe las señales de control para la implementación secuencial de la división con restauración.

- Un medio de cálculo aritmético para obtener los múltiplos impares del divisor.

- Un medio para capturar k dígitos del dividendo.

- Medios para concatenar registros de memoria.

- Medios para ajustar el resto.

- Medios de memoria para almacenar

- un registro X que corresponde al dividendo X,

- un registro sX que corresponde a k bits del dividendo X,

- un registro Y que corresponde al divisor Y,

- un conjunto de 2^k-1 registros que corresponden a los múltiplos impares del divisor Y: 3Y, 5Y, ... (2^k-1)Y,

- un registro rem que corresponde al resto parcial R(p),

- un registro new_rem que corresponde al nuevo resto parcial R(p+1),

- un registro R que corresponde al resto final,

- un registro new_q que corresponde a k dígitos del cociente,

- un registro Q que corresponde al cociente.

13. Circuito para implementar un implementar un método de división sin restauración que comprende una célula de base 2^k en la que se introducen los múltiplos impares del divisor, el resto parcial y k bits del dividendo y genera como resultado k bits de cociente y un nuevo resto para la siguiente etapa en donde la arquitectura es paralela.

14. Circuito según la reivindicación anterior caracterizado porque comprende:

- un conjunto [n/k]+1 células de base 2^k

- Un medio de cálculo aritmético para obtener los múltiplos impares del divisor.

- Medios para sincronizar el funcionamiento de las células 2^k.

- Un medio para capturar k dígitos del dividendo.

- Medios para concatenar registros de memoria.

- Medios para ajustar el resto.

- Medios de memoria para almacenar

- un registro X que corresponde al dividendo X,

- un registro Y que corresponde al divisor Y,

- un conjunto de 2^k-1 registros que corresponden a los múltiplos impares del divisor Y: 3Y, 5Y, ... (2^k-1)Y,

- un registro R que corresponde al resto final,

- un registro q que corresponde a k dígitos del cociente,

- un registro Q que corresponde al cociente.

15. Conjunto de instrucciones que, cuando son interpretadas por un medio programable, hacen que este medio realice un método según cualquiera de las reivindicaciones 1 a 3.

16. Conjunto de instrucciones cuya interpretación por un medio programable hacen que un medio de lógica programable configure una célula de recurrencia según cualquiera de las reivindicaciones 4 a 10.

17. Conjunto de instrucciones para implementar un método en un medio programable que, cuando son interpretadas por dicho medio programable, hacen que un medio de lógica programable configure un circuito divisor según cualquiera de las reivindicaciones 11 a 14.

18. Conjunto de instrucciones para implementar un método en un medio programable que, cuando son interpretadas por dicho medio programable, hacen que este medio realice dicho método según cualquiera de las reivindicaciones 1 a 3.

19. Producto que comprende un conjunto de instrucciones registradas en un medio legible y ejecutables en un medio programable, cuya ejecución comprende que dicho medio programable realice cualquiera de las reivindicaciones 15 a 18.