1. Dispositivo para la enseñanza de los numerales que divide los numerales en varios niveles,

cada uno de los cuales va impreso en una pieza distinta. La primera pieza (1), la de mayor tamaño, puede ser de forma rectangular, circular, poligonal o irregular, y va situada en la parte inferior. La segunda pieza (2) es de forma circular y se sitúa encima de la primera pieza. La tercera pieza (3) a partir de una forma circular primaria de un diámetro similar al de la segunda pieza, lleva un entrante que permite ver elementos situados en la segunda pieza. La cuarta pieza (4) es de forma circular. Todas las piezas llevan un agujero central por el que están unidas a las demás por medio de un remache, hoyuelo, etc. que sirve de eje (5) y permite que unas piezas puedan girar con respecto a otras. En la periferia de la primera pieza, dispuestas de forma más o menos circular, irán las centenas (nivel 1). En la periferia de la segunda pieza se sitúan los numerales que van del 10 al 19 ó del 11al 19 en letras, (nivel 2/3). En la periferia de la taceta pieza se sitúan las decenas (nivel 2). En la periferia de la cuarta pieza se sitúan las unidades (nivel 3). En esta misma pieza, podrá situarse el nivel 4: mil, entre paréntesis, debajo de cada número del tercer nivel y a cierta distancia de él, también en esta pieza, podrá situarse 1.000.000 entre paréntesis debajo de 1.000, siempre escritos por sus nombres en letras. Girando unas piezas con respecto a otras se pueden relacionar los numerales de los distintos niveles a fin de construir numerales compuestos.

2. Dispositivo para la enseñanza de los numerales según reivindicación anterior en el que la primera pieza (1), la de mayor tamaño, sea de forma circular.

3. Dispositivo para la enseñanza de los numerales según reivindicación 1, el que la primera pieza (la de mayor tamaño), tenga la forma de un polígono regular.

4. Dispositivo para la enseñanza de los numerales según reivindicación 1, en el que la primera pieza (la demayor tamaño), tenga una forma irregular.

5. Dispositivo para la enseñanza de los numerales según cualquiera de las reivindicaciones anteriores en el que la cuarta pieza (4) lleve un saliente.

6. Dispositivo para la enseñanza de los numerales según cualquier reivindicación de la 1 a la 4 en el que la cuarta pieza lleve dos salientes.

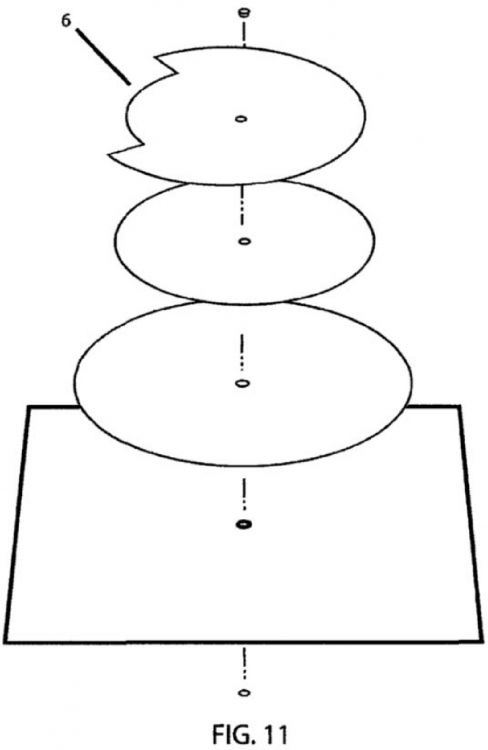
7. Dispositivo para la enseñanza de los numerales según cualquier reivindicación de la 1 a la 4 en el que la cuarta pieza lleve un entrante (6) y sea de un diámetro similar a la tercera y en el que la tercera pieza sea circular.

8. Dispositivo para la enseñanza de los numerales según cualquiera de las reivindicaciones anteriores formado por solo tres piezas al no existir la tercera pieza ni el nivel segundo/tercero que iría en esa pieza, y en el que el segundo nivel se sitúe en la segunda pieza y el tercero y el cuarto nivel se sitúen en la tercera.

9. Dispositivo para la enseñanza de los numerales según cualquier reivindicación de la 1 a la 7 en elque exista una quinta pieza (7) circular, más pequeña, encima de las otras cuatro y en la que se sitúen los numerales del cuarto nivel

Dispositivo para la enseñanza de los numerales.

Objeto de la invención

La presente invención se refiere a un dispositivo que pretende ser un auxiliar en la enseñanza de los numerales del inglés y de otros idiomas, simplificando la tarea mental de relacionar los numerales para crear otros distintos, dividiendo los numerales en varios niveles que se combinan entre si desde los niveles inferiores hacia los superiores.

Antecedentes de la invención

Existen algunas invenciones para aprender a enseñar los números a los niños que consisten en bolas con los números impresos (CN201004280) (Y). Otros proponen unas fichas compuestas de tres partes que permitirían ver un número y su nombre o una imagen y un nombre (US2006078865) (A1). Otros permiten aprender series de números que van sujetos a las distintas partes de un par de guantes o con una serie de anillos (GB2451223) (A). Otros proponen una serie de tablillas con los numerales del 1 al 20, para ayudar a los niños en su aprendizaje y en su uso (CN2541917) (Y).

Descripción de la invención

La presente invención se refiere a un mecanismo útil para la enseñanza de los numerales, que permite combinarlos y relacionarlos entre si en cuatro niveles de numerales básicos: el de las centenas, el de las decenas, el de las unidades, y el de los grandes numerales, para construir los numerales compuestos.

En un primer nivel tendremos las centenas, en el caso del inglés: one hundred and, two hundred and, three hundred and, four hundred and, five hundred and, six hundred and, seven hundred and, eight hundred and, nine hundred and.

En un segundo nivel tendremos las decenas: ten, twenty, thirty, forty, fifty, sixty, seventy, eighty, ninety.

En un segundo/tercer nivel situaremos los números que van del 10 al 19 o del 11 al 19: ten, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eightecn, nineteen. Estos números son en realidad una especie de aleación entre los números del segundo y del tercer nivel.

En el tercer nivel tendremos a las unidades: one two, three, four, five, six, seven, eight, nine.

En el cuarto nivel tenemos varios niveles de numerales superiores que por su escaso uso en la lengua corriente (excepto thousand y million) agrupamos en un solo nivel, son los siguientes: thousand (Con el cual se forman los millares a partir de los niveles inferiores) y los grandes numerales: million, billion, trillion, cuadrillion, quintillion, sextillion, septillion, octillion, nonillion, etc. (Los grandes numerales, a partir del trillón son muy poco usados en la lengua corriente, utilizándose en su lugar su equivalente en potencias de 10 y más raramente de 1.000.000).

Relacionando unos niveles con otros se pueden formar todos los números del uno al mil, y todas las unidades de millar hasta un millón. Pero la forma de construir los números será siempre desde los niveles inferiores hacia los superiores. Por ejemplo, podemos construir, "two hundred and nine" (nivel 1, nivel 3). Pero no podemos construir: "nine two hundred" (nivel 3, nivel 1). Sin embargo, una vez se ha llegado al 4º nivel, es posible regresar a cualquiera de los niveles inferiores mentalmente o utilizando un segundo dispositivo para volver a subir otra vez, y completar un numero de 4 a 6 cifras como 567.342: five hundred and (nivel 1), sixty (nivel 2), seven (nivel 3), thousand (nivel 4), three hundred and (nivel 1), forty (nivel 2), two (nivel 3).

Estos niveles pueden ir en varios dispositivos, por ejemplo: un dispositivo formado por cuatro piezas, (o eventualmente por cinco). La primera pieza (la de mayor tamaño) puede ser de varias formas: circular, cuadrada, etc. y va situada en la parte inferior. La segunda pieza es de forma circular y se sitúa encima de la primera pieza. La tercera pieza a partir de una forma circular primaria de un tamaño similar al de la segunda pieza, lleva un entrante que permite ver elementos situados en la segunda pieza. La cuarta pieza es de forma circular. Todas las piezas tienen un agujero central por el que se unen a las demás piezas por medio de un remache, hoyuelo o algo similar, que permite que giren unas con respecto a otras. En la periferia de la primera pieza se sitúan, formando un círculo, los numerales del nivel uno (centenas), en el caso del inglés: one hundred and, two hundred and, three hundred and, four hundred and, five hundred and, six hundred and, seven hundred and, eight hundred and, nine hundred and. En la periferia de la segunda pieza se sitúan los numerales del segundo/tercer nivel: ten, eleven, twelve, thirteen, fourteen, fifteen, sixteen, seventeen, eighteen, nineteen (el número 10 en este nivel es optativo y puede excluirse). En la periferia de la tercera pieza se sitúan los numerales del segundo nivel: ten, twenty, thirty, forty, fifty, sixty, seventy, eighty, ninety. En la periferia de la cuarta pieza se sitúan los numerales del tercer nivel: one two, three, four, five, six, seven, eight, nine. Los numerales del cuarto nivel, thousand, million, etc. pueden situarse en esta misma cuarta pieza de la siguiente forma: thousand entre paréntesis debajo de cada número del tercer nivel y a cierta distancia de él. También en esta pieza se situará million, entre paréntesis, debajo de thousand y a cierta distancia de él. Otra alternativa es situar el cuarto nivel en una quinta pieza, en la periferia de la cual además de thousand y million se situarán: billion, trillion y otros grandes numerales. Girando unas piezas con respecto a otras se pueden relacionar los numerales de los distintos niveles a fin de construir numerales complejos. Por ejemplo: podemos girar la primera pieza, en ella están los numerales del primer nivel, buscaremos en ella six hundred and; en la tercera pieza buscaremos forty (segundo nivel); en la tercera pieza buscaremos nine (tercer nivel). De esta forma habremos formado: six hundred and forty nine, siguiendo la norma de ir siempre de los niveles inferiores a los superiores y no al revés. En algunos casos, para idiomas diferentes, las piezas podrán tener algunos salientes que cambien su forma. También se podrán utilizar otros soportes como fichas, dispositivos tridimensionales, etc. que contengan los numerales de los distintos niveles, para luego combinarlos siempre desde los niveles inferiores a los superiores. En algunos casos, sobre todo para enseñar a los niños, los dispositivos llevarán solamente los tres primeros niveles. En otros casos, para físicos, matemáticos, etc. los dispositivos llevarán los grandes numerales: million, billion, trillion, cuadrillion, quintillion, sextillion, septillion, octillion, nonillion etc.

Los números incluidos en cada nivel pueden variar ligeramente dependiendo del idioma.

Descripción de los dibujos

Figura 1.- Vista desde un ángulo superior (de 45 grados) en la que podemos ver separadas las distintas piezas.

Figura 2.- Vista superior del conjunto en la que podemos ver: la primera pieza (1), la segunda pieza (2), la tercera pieza (3) con un entrante (6), la cuarta pieza (4), y el eje central (5).

Figura 3.- Vista superior de la primera pieza (1).

Figura 4.- Vista superior de la segunda pieza (2).

Figura 5.- Vista superior de la tercera pieza (3).

Figura 6.- Vista superior de la cuarta pieza (4).

Figura 7.- Vista desde un ángulo superior (de 45 grados) en la que podemos ver separadas las distintas piezas y en la que existe un saliente en la cuarta pieza (4). La primera pieza (1) es circular.

Figura 8.- Vista desde un ángulo superior (de 45 grados) en la que podemos ver separadas las distintas piezas y en la que existen dos salientes en la cuarta pieza (4).

Figura 9.- Vista desde un ángulo superior (de 45 grados) en la que podemos ver separadas las distintas piezas y en las que existe un saliente en la segunda pieza (2). Existe una quinta pieza circular (7).

Figura 10.- Vista desde un ángulo superior (de 45 grados) en la que podemos ver separadas las distintas piezas y en la que solo hay tres piezas.

Figura 11.- Vista desde un ángulo superior (de 45 grados) en la que podemos ver separadas las distintas piezas y en la que existe un entrante (6) en la cuarta pieza.

Modos de realización de la invención

La presente invención se ilustra mediante los siguientes ejemplos, los cuales no pretenden ser limitativos de su alcance.

Ejemplo 1

Dispositivo formado por cuatro piezas. La primera pieza (la de mayor tamaño) es de forma rectangular y va situada en la parte inferior. La segunda pieza es de forma circular...

1. Dispositivo para la enseñanza de los numerales que divide los numerales en varios niveles, cada uno de los cuales va impreso en una pieza distinta. La primera pieza (1), la de mayor tamaño, puede ser de forma rectangular, circular, poligonal o irregular, y va situada en la parte inferior. La segunda pieza (2) es de forma circular y se sitúa encima de la primera pieza. La tercera pieza (3) a partir de una forma circular primaria de un diámetro similar al de la segunda pieza, lleva un entrante que permite ver elementos situados en la segunda pieza. La cuarta pieza (4) es de forma circular. Todas las piezas llevan un agujero central por el que están unidas a las demás por medio de un remache, hoyuelo, etc. que sirve de eje (5) y permite que unas piezas puedan girar con respecto a otras. En la periferia de la primera pieza, dispuestas de forma más o menos circular, irán las centenas (nivel 1). En la periferia de la segunda pieza se sitúan los numerales que van del 10 al 19 o del 11 al 19 en letras, (nivel 2/3). En la periferia de la tercera pieza se sitúan las decenas (nivel 2). En la periferia de la cuarta pieza se sitúan las unidades (nivel 3). En esta misma pieza, podrá situarse el nivel 4: mil, entre paréntesis, debajo de cada número del tercer nivel y a cierta distancia de él, también en esta pieza, podrá situarse 1.000.000 entre paréntesis debajo de 1.000, siempre escritos por sus nombres en letras. Girando unas piezas con respecto a otras se pueden relacionar los numerales de los distintos niveles a fin de construir numerales compuestos.

2. Dispositivo para la enseñanza de los numerales según reivindicación anterior en el que la primera pieza (1), la de mayor tamaño, sea de forma circular.

3. Dispositivo para la enseñanza de los numerales según reivindicación 1, en el que la primera pieza (la de mayor tamaño), tenga la forma de un polígono regular.

4. Dispositivo para la enseñanza de los numerales según reivindicación 1, en el que la primera pieza (la de mayor tamaño), tenga una forma irregular.

5. Dispositivo para la enseñanza de los numerales según cualquiera de las reivindicaciones anteriores en el que la cuarta pieza (4) lleve un saliente.

6. Dispositivo para la enseñanza de los numerales según cualquier reivindicación de la 1 a la 4 en el que la cuarta pieza lleve dos salientes.

7. Dispositivo para la enseñanza de los numerales según cualquier reivindicación de la 1 a la 4 en el que la cuarta pieza lleve un entrante (6) y sea de un diámetro similar a la tercera y en el que la tercera pieza sea circular.

8. Dispositivo para la enseñanza de los numerales según cualquiera de las reivindicaciones anteriores formado por solo tres piezas al no existir la tercera pieza ni el nivel segundo/tercero que iría en esa pieza, y en el que el segundo nivel se sitúe en la segunda pieza y el tercero y el cuarto nivel se sitúen en la tercera.

9. Dispositivo para la enseñanza de los numerales según cualquier reivindicación de la 1 a la 7 en el que exista una quinta pieza (7) circular, más pequeña, encima de las otras cuatro y en la que se sitúen los numerales del cuarto nivel.