MÉTODO PARA LA OPTIMIZACIÓN DE UNA SEÑAL DE EXCITACIÓN O CONTROL TRANSITORIA QUE ACTÚA EN UN SISTEMA VIBRATORIO CON EL FIN DE REDUCIR LA VIBRACIÓN RESIDUAL GENERADA.

Método para la optimización de una señal de excitación o control transitoria que actúa en un sistema vibratorio con el fin de reducir la vibración residual generada.

La presente invención tiene por objetivo la reducción de vibraciones residuales provocadas por la excitación de una señal transitoria en sistemas vibratorios con comportamiento lineal. Esta señal corresponde, por ejemplo, a una ley de movimiento de una inercia o de una fuerza excitadora.

Partiendo de una señal base a optimizar, se parametriza ésta con tantos parámetros como ecuaciones tiene el sistema definido por la condición necesaria suficiente de vibración residual nula. Esta equivale, para un modo propio de vibración, a un sistema implícito de dos ecuaciones con dos incógnitas. En sistemas de n modos propios vibratorios, se incluyen 2n parámetros en dicha señal para la resolución de un sistema de 2n ecuaciones.

Se incluye una particularización especialmente indicada para señales cuyo valor máximo se requiera constante durante un tiempo, utilizadas en leyes de desplazamiento de doble detención para mecanismos leva-palpador o en consignas de velocidad en sistemas de control.

Método para la optimización de una señal de excitación o control transitoria que actúa en un sistema vibratorio con el fin de reducir la vibración residual generada.

Sector de la técnica La invención se encuadra en el sector técnico de vibraciones mecánicas, más concretamente, en el estudio de la reducción de vibraciones residuales en sistemas genéricos vibratorios con comportamiento lineal, después de ser sometidos a algún tipo de señal transitoria, por ejemplo, en transitorios de movimiento de una inercia sobre ellos o transitorios de fuerzas excitadoras.

Estado de la técnica

El estudio de la reducción de oscilaciones residuales después de la entrada de una señal transitoria tiene su origen en movimientos punto a punto de inercias, como por ejemplo en grúas, pórticos o aplicaciones sobre manipuladores robóticos con más o menos flexibilidad en sus elementos, y tiene como objetivo la mejora en la precisión de los movimientos sin precisar tiempos de demora elevados y/o el aumento de sus prestaciones para la reducción de costes de explotación en su funcionamiento.

Existen dos áreas de estudio en cuanto a la reducción de vibraciones residuales. La primera está basada en la síntesis de señales que definen el transitorio. La segunda está basada en sistemas de control activo de vibraciones. Dentro del primer grupo, las técnicas más estudiadas para la síntesis de estas señales que definen los transitorios, ya sean de movimiento o fuerza, corresponden a:

El perfilado de señales de control mediante convolución de un tren de impulsos o pulsos con una señal de referencia conocida: La oscilación generada en el sistema por un impulso es cancelada por superposición de la oscilación generada por un segundo impulso. Fue desarrollada por:

Ref. 1: Singer, N.C., Seering, W.P. (patente US-4916635 y 13114491) .

La descripción de dicho método expresado por medio de vectores giratorios corresponde a:

Ref. 2: Singhose, W.E., Seering, W.P., Singer, N.C. (1990) , Shaping Inputs to Reduce Vibration: A Vector Diagram

Approach. IEEE Proceedings of the International Conference on Robotics and Automation, Cincinnati, OH, USA, 2:

922-927. Ref. 3: Singhose, W.E., Seering, W.P., Singer, N.C. (1994) , Residual Vibration Reduction Using Vector Diagrams to Generate Shaped Inputs. ASME Journal of Mechanical Design, 116: 654-659.

El uso de impulsos negativos para reducir el tiempo de transitorio fue desarrollado por:

Ref. 4: Singhose, W.E., Seering, W.P., Singer, N.C. (1994) , Design and Implementation of Time-Optimal Negative Input Shapers. ASME Winter Annual Meeting, Chicago, IL, USA: 151-157. La condición necesaria y suficiente para que no exista vibración residual es que la transformada de Laplace de la

señal transitoria de excitación tenga módulo nulo en los polos del sistema. Esta demostración fue desarrollada por:

Ref. 5: Bhat, S.P., Miu, D.K. (1990) , Precise Point-to-Point Positioning Control of Flexible Structures. ASME Journal of Dynamic Systems, Measurement, and Control, 112 (4) : 667-674. La reducción de la respuesta del sistema mediante filtrado digital de la señal de control en la banda de frecuencias

de interés corresponde a: Ref. 6: Oppenheim, A.V. y Schafer, R.W. (1975) Digital Signal Processing. USA: Prentice-Hall, Inc. Ref. 7: Singhose, W.E., Singer, N.C., Seering, W.P. (1995) , Comparison of Command Shaping Methods for

Reducing Residual Vibration. Proceedings of the 1995 European Control Conference) . El diseño de filtros específicos digitales para la reducción de vibraciones residuales fue implementado por: Ref. 8: Magee, D.P., Book, W.J. (1998) , Optimal Filtering to Minimize the Elastic Behavior in Serial Link

Manipulators. Proceedings of the American Control Conference, Philadelphia, Pennsylvania: 2637-2642.

El filtrado por medio de funciones base afectadas de una exponencial negativa corresponde a:

Ref. 9: Zhou, L., Misawa, E.A. (Patent Application US2007/0067049)

La definición de señales por inversión de la dinámica del sistema consiste en la generación de la señal de control partiendo de las ecuaciones dinámicas del sistema invertidas, y de la respuesta de salida deseada y fue desarrollada por:

Ref. 10: Asada, Haruhiko, Ma, Zeng-Dong, y Tokumaru, Hidekatsu, (1987) , Inverse Dynamics of Flexible Robot Arms of Trajector y Control. Moldeling and Control of Robotic Manipulators, ASME 1987 Winter Annual Meeting.

La presente invención constituye una nueva aportación a este sector de la técnica. En general, los métodos presentados de otros autores focalizan su trabajo en la optimización de la duración del transitorio. Sin embargo, la forma que toma la señal no es regular, ni presenta una zona máxima plana, con lo que en determinadas aplicaciones se puede comprometer la función original del sistema. Se expone el desarrollo teórico y las conclusiones a partir de las cuales se podrá generar una determinada señal de excitación o control con el objetivo de reducir las vibraciones residuales, en sistemas dinámicos con comportamiento lineal. El método presentado, aunque de carácter universal en sus posibles aplicaciones, está especialmente indicado para los casos en donde se requiera que la forma original de la señal base se conserve, salvo por sus relaciones de aspecto, como por ejemplo cuando se requiere que la amplitud máxima se mantenga constante durante un cierto tiempo.

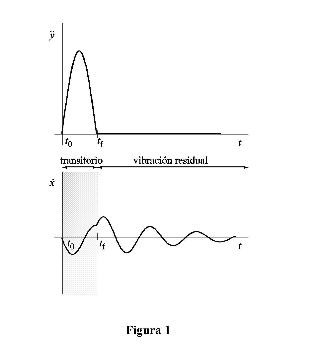
Descripción de las figuras Figura 1: Significado de vibración residual.

Figura 2: Sistema genérico de un grado de libertad vibratorio.

Figura 3: Optimización de una señal base con los parámetros a1 y a2.

Figura 4: Utilización del eje temporal para la inclusión de parámetros incógnita Ti y del eje de ordenadas para la inclusión de parámetros incógnita aj.

Figura 5: Ejemplo de inclusión de parámetros incógnita en una señal de excitación.

Figura 6: Ejemplo de optimización de señal para un sistema de un modo propio de vibración.

Figura 7: Sistema genérico de dos grados de libertad vibratorios.

Figura 8: Ejemplo de optimización de señal para un sistema de dos modos propios de vibración.

Descripción detallada de la invención

Fundamento teórico Se define vibración residual de la respuesta de un sistema mecánico vibratorio, aquella respuesta vibratoria que se observa a partir del instante de tiempo en el que acaba la señal excitadora, supuesta ésta transitoria de duración finita (figura 1) . La ausencia de vibración residual de la respuesta del sistema implica, por tanto, una duración temporal de la señal excitadora igual a la duración de la respuesta vibratoria del sistema.

Según demuestran Bhat y Miu (Ref. 5) , la condición necesaria y suficiente para que no exista vibración residual es que la transformada de Laplace de la señal transitoria de excitación tenga módulo nulo en los polos del sistema. Haciendo referencia al sistema genérico de la figura 2, su ecuación de movimiento se puede expresar como mxt t () myt

xx () + c () + kxt =-xx () (1.1)

donde x e y son las coordenadas indicadas en la figura y m representa la masa del sistema, k la rigidez del muelle y c el coeficiente de amortiguamiento. Esta expresión puede reescribirse como 2 yt

() t + 2 (2 f) () t + (2 f) xt () =-xx () (1.2)

donde f =1 (2 l )

es la frecuencia natural del sistema y =c 2 mkes su razón de amortiguamiento.

La función de transferencia definida por la transformada de Laplace de la función x (t) /y (t) viene dada por

() -s

Xs = 22 (1.3) () s + 4 fs+ (2 f)

Ys

Asumiendo un comportamiento vibratorio, los polos del sistema son s1, 2 =-2 f0 ±j2 f (1.4)

d

donde f = f 1-2 es la frecuencia de oscilación. En general, la ecuación de movimiento de un sistema con d 0

comportamiento lineal y con un modo propio de vibración se puede escribir como () +cqt () +kqt = ()

mqt xx x () ht (1.5)

donde q describe la coordenada de salida del sistema, y h (t) corresponde a la función temporal de entrada. Por tanto, los polos del sistema coinciden con los descritos en (1.4) .

La transformada de Laplace de un señal transitorio y (t) definido entre los instantes temporales t0 y tf (t0 º 0 y tf º 0) es tf -st

() = yt ( ) e (1.6)

Ys dt

t

Tal y como se ha indicado en la condición necesaria suficiente enunciada, se evalúa Y (s) en los polos del sistema y se 10 iguala a cero tYs ) = f yt ( ) e -- (2 f0 ±j2 ft d) dt=0 (1.7)

( 1, 2

t

Desarrollando esta expresión se obtiene f2 ft f2 ft

...

Método para optimizar señales transitorias de excitación o control en sistemas dinámicos con comportamiento lineal de al menos un grado de libertad vibratorio para reducir vibraciones residuales que comprende: la determinación de las n frecuencias propias f0i del sistema vibratorio y de las n razones de amortiguamiento modales respectivas (i, cuya influencia se desee reducir en la vibración residual, mediante ensayo o mediante la resolución de las ecuaciones de movimiento; la obtención de una señal parametrizada y (t) mediante la inclusión de 2n parámetros incógnita en la señal base yb (t) de excitación que se desea optimizar y de p parámetros adicionales a los primeros correspondientes a los p requerimientos funcionales que se desean cubrir; la resolución del sistema de ecuaciones formado por 2n+p ecuaciones, con 2n ecuaciones según t

f2 ft

y ( ) e ti 0 cos (2 ft t = 0

i di) d i= 1, ..., n t

t

f2 ft

i 0i

yt di) d

( ) e sin (2 ft t = 0 i= 1, ..., n t

y con p ecuaciones según gyt