Procedimiento de determinación de la constante de criticidad en un reactor nuclear subcrítico.

Procedimiento de determinación de la constante de criticidad en un reactor nuclear subcrítico.

Procedimiento para la determinación de la constante de criticidad (keff) de un reactor nuclear subcrítico que consiste en buscar relaciones unívocas entre un estimador y la constante de criticidad. Comprende modelar el sistema subcrítico con un código de simulación neutrónica utilizando un modelo de referencia de la geometría y la composición del reactor y calcular la reactividad del sistema cuando se varían los parámetros característicos. El procedimiento es aplicable a cualquier estimador y no requiere el conocimiento de los parámetros cinéticos del sistema.

Procedimiento de determinación de la constante de criticidad en un reactor nuclear subcrítico.

Sector de la técnica La presente invención pertenece al campo de la física nuclear. En particular, la invención se refiere a un procedimiento para la determinación de la constante de criticidad (keff) de un reactor nuclear subcrítico guiado por acelerador.

Estado de la técnica El concepto de sistema subcrítico guiado por acelerador (ADS por sus siglas en inglés) ha sido objeto de considerable interés desde los años 90, debido a su potencial para reducir el volumen y la radiotoxicidad del

combustible nuclear irradiado. Más concretamente, la utilidad de los ADS viene dada por su capacidad para fisionar el plutonio y el americio presentes en el combustible nuclear irradiado, de cuya actividad a largo plazo son los principales responsables, y así transmutarlos en productos de fisión de vida más corta.

Un ADS consiste en un reactor nuclear subcrítico acoplado a una fuente externa de neutrones. Con esta configuración se elimina (o al menos se relaja) el requerimiento de estabilidad necesario en los reactores críticos convencionales, lo que permite cargar cantidades superiores de plutonio y actínidos minoritarios. La constante de criticidad (keff) se define como la relación entre el número de neutrones creados en un sistema mediante fisiones y el número de neutrones perdidos mediante captura neutrónica o escape geométrico. Si keff<1, el sistema se dice subcrítico y la población neutrónica se extingue al cabo de un cierto tiempo. Si keff=1 el sistema se dice crítico y la población neutrónica y la potencia del sistema se mantiene constante en el tiempo; este es el modo de operación normal de los reactores nucleares convencionales. Finalmente, si keff>1 el sistema se dice supercrítico y la población neutrónica y la potencia crecen de forma exponencial en el tiempo.

La reactividad es un concepto alternativo a la constante de criticidad y se define como: keff -1

p=

keff

En un sistema crítico, p=0; en un sistema subcrítico, p<0 y en un sistema supercrítico p>0.

Para describir el comportamiento temporal (cinético) de un sistema ADS se usa habitualmente el modelo de cinética puntual. Éste se basa en considerar que el flujo de neutrones en el reactor es separable en una componente espacial y otra temporal. Su aplicabilidad en sistemas reales viene determinada por el cumplimiento de esta hipótesis.

La mayoría de los ADS contemplan valores de keff=0.95-0.98. Con estos valores de keff, se tiene que por cada neutrón de la fuente se producen por fisiones en el sistema subcrítico entre 20 y 100 neutrones adicionales, de forma que la potencia generada en el conjunto subcrítico es mucho mayor que la necesaria para el funcionamiento del acelerador y el sistema completo tiene un balance energético positivo.

Una condición de seguridad básica para operar un ADS es garantizar que se puede monitorizar la keff del sistema.

Por esta razón se han llevado a cabo en los últimos años una serie de experimentos en conjuntos subcríticos de potencia cero, con el fin de validar experimentalmente diferentes técnicas para la monitorización de la reactividad. En la siguiente tabla se presentan de forma resumida algunos datos de estos experimentos.

Experimento Combustible Moderador Fuente de neutrones Acelerador

FEAT (CERN) Unat H2O Espalación en U Sincrotrón, p

MUSE (CEA) MOX (25% Pu) --- D-T, D-D Electrostático, D

Guinevere (SCK-CEN) Umet (30%) --- D-T, D-D Electrostático, D

Energy + Trasmutation (JINR) Unat --- Espalación en Pb Sincrotrón, p, D

Yalina-Thermal (JIPNR) UO2 (10%) Polietileno D-T, D-D Electrostático, D

Yalina-Booster (JIPNR) UO2 (36%) UO2 (10%) Polietileno D-T, D-D Electrostático, D

KUCA (KURRI) Umet (93%) Polietileno Espalación en W Sincrotrón FFAG, p

RACE (IAC) Umet (20%) H2O Fotoneutrones LINAC, e

Venus-1 (CIAE) Unat -LEU Polietileno D-T, D-D Electrostático, D

Las medidas realizadas en estos experimentos con objeto de monitorizar la reactividad son fundamentalmente de dos tipos: con fuente de neutrones pulsada (Pulsed Neutron Source, PNS) y con fuente de neutrones continua con interrupciones cortas (beam trips) .

Hay dos métodos fundamentales para determinar la reactividad de un sistema subcrítico a partir de experimentos con una fuente de neutrones pulsada. El primero se conoce como método de la constante de decaimiento de los neutrones inmediatos, o simplemente, método de las pendientes. Este método se deriva del modelo de la cinética puntual y de él se obtiene una relación entre la reactividad del sistema y la constante de decaimiento de los neutrones inmediatos, a:

p=A a+J

eff eff

Donde Ieff y ºeff son, respectivamente, el tiempo medio entre generaciones neutrónicas y la fracción de neutrones retardados, conocidos globalmente como los parámetros cinéticos del sistema.

El segundo método para determinar la reactividad de un sistema subcrítico a partir de los resultados de un experimento con fuente de neutrones pulsada se conoce como método de las áreas o método de Sjöstrand. Al igual que el anterior, este método deriva del modelo de la cinética puntual, del que se obtiene que la reactividad del sistema está relacionada con el cociente entre el área contenida bajo la curva de evolución de los neutrones inmediatos, Ap, y los retardados, Ad.

Ap

p=-Jeff

Ad En el caso de los experimentos con beam-trips se utilizan también las dos técnicas anteriores aunque en el caso del método de las áreas (que con beam-trips se denota habitualmente como método de Source-Jerk) la expresión de la reactividad presenta la forma:

p=-J n0 -n1

eff

n

Donde n0 es el flujo de neutrones antes de la interrupción y n1 el flujo de neutrones después de dicha interrupción.

En sistemas reales, sin embargo, la cinética puntual se ve alterada por la presencia de efectos espacio-temporales complejos, lo que hace necesaria la aplicación de técnicas de corrección a los valores medidos para obtener el valor de la reactividad del sistema.

Diversas técnicas han sido propuestas por diferentes autores para resolver este problema. Estas técnicas incluyen la utilización de factores de corrección, calculados mediante técnicas deterministas o Monte Carlo y modelos de cinética multi-región (Jammes, C. et al., 2006, “Advantage of the area-ratio pulsed neutron source technique for ADS reactivity calibration”, Nuclear Instruments and Methods in Physics Research A 562, 778-784; C. Berglöf et al., 2010, “Spatial and Source Multiplication Effects on the Area ratio Reactivity Determination Method in a Strongly Heterogeneous Subcritical System”, Nuclear Science and Engineering 166, 134-144) o la utilización del tiempo entre generaciones neutrónicas (Perdu, F. et al., 2003 “Prompt reactivity determination in a subcritical assembly through the response to a Dirac pulse”, Progress in Nuclear Energy 42, 107-120) . Sin embargo, estos métodos presentan los inconvenientes de que es necesario conocer los parámetros cinéticos del sistema para aplicarlos, parámetros que no siempre son medibles, ya que su medida se realiza con el reactor en estado crítico. Además, es deseable disponer de un mismo procedimiento que se pueda utilizar tanto con fuentes pulsadas (PNS) como con interrupciones (beamtrips ) .

Objeto de la invención

El procedimiento de la invención consiste en buscar relaciones unívocas entre un estimador y la constante de criticidad. Por estimador se entiende cualquier parámetro medible mediante detectores que esté relacionado con la constante de criticidad del sistema.

La existencia de dicha relación unívoca no está garantizada para todo el rango de reactividades y posibles valores de dichos estimadores, pero existe dentro de un determinado rango cerca de las condiciones experimentales. La forma funcional de esta relación puede obtenerse a partir de simulaciones del sistema, mediante un conjunto de variaciones de varios parámetros característicos del sistema. Los parámetros que deben variarse son aquellos cuya variación da lugar a variaciones de la reactividad de más de 100 p.c.m, como por ejemplo, pero no de forma exclusiva, las dimensiones en las tres direcciones del espacio y posiciones relativas de cada uno de los elementos que componen el sistema; las temperaturas, presiones, densidades y composiciones isotópicas, así como la distribución espacial dentro del sistema de estos elementos; el número de elementos repetidos y cualquiera de los datos nucleares utilizados en las simulaciones del...

1. Procedimiento para la determinación de la constante de criticidad (keff) de un reactor nuclear subcrítico que comprende los siguientes pasos:

a) colocar detectores de neutrones en distintas posiciones dentro del reactor para obtener la evolución temporal de las tasas de contaje;

b) a partir de la evolución de estas tasas de contaje obtener el valor de los estimadores de la reactividad

X para cada posición de los detectores;

pos, exp

c) modelar el sistema subcrítico con un código de simulación neutrónica utilizando un modelo de referencia de la geometría y la composición del reactor;

d) calcular con el mismo código de simulación el valor de la reactividad p= (k , 0 -1) k de este 0 eff eff , 0

modelo de referencia, donde Keff es la constante de criticidad del sistema; e) para el mismo modelo de referencia, calcular con el código de simulación el valor de los mismos estimadores para cada una de las posiciones de los detectores, X ;

pos, 0

f) partiendo del modelo de referencia, definir nuevos modelos modificando los parámetros característicos del sistema;

g) para cada uno de estos modelos modificados calcular con el código de simulación los valores de la reactividad p y los estimadores X para cada una de las posiciones de los detectores;

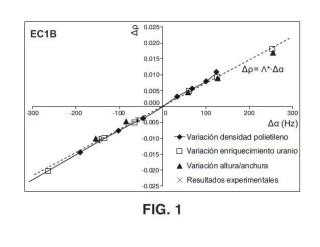
pos h) para cada posición experimental, representar los valores así obtenidos de la variación de la reactividad M= - frente a la variación del estimador ;

ppp0 MX pos =X pos -X pos, 0 i) realizar un ajuste lineal de los pares de puntos (MX, Mp) a la expresión Mp=a MX para

pos pos pos calcular el parámetro apos correspondiente a cada posición experimental de los detectores;

j) estimar los errores sistemáticos cometidos en los parámetros apos calculados para cada posición realizando tantos ajustes lineales como parámetros característicos del sistema se hayan modificado, con los pares de puntos (MX, Mp) obtenidos modificando cada uno de los parámetros del sistema por

pos separado y tomar como error sistemático la máxima diferencia del valor de apos calculado anteriormente con los valores obtenidos con cada parámetro por separado;

k) calcular el valor experimental para la reactividad del sistema pexp y su error mediante la expresión p =p+a (X -X , 0 ) .

exp 0 pos pos, exp pos 2. Procedimiento según la reivindicación 1 caracterizado porque el estimador es la relación de áreas entre los neutrones retardados e inmediatos Ap

Ad , obteniéndose Ad multiplicando el valor de la tasa de contaje de neutrones retardados por el tiempo entre dos pulsos consecutivos de la fuente y A de la diferencia entre el

p

número total de cuentas en el intervalo entre dos pulsos consecutivos de la fuente y este valor de Ad , procedimiento que comprende los siguientes pasos: a) para cada uno de los modelos definidos en f, calcular con el código de simulación el valor de la reactividad del sistema p y los valores de (AA ) para cada una de las posiciones de los p

d

pos detectores;

b) para cada posición de los detectores, representar los valores así obtenidos de M=

ppp frente a los valores de M (AA ) = (AA ) - (AA ) ;

p

dp

dp

d

pos pos pos, 0

c) realizar un ajuste lineal de los pares de puntos (M (AA ) , Mp) a la expresión p

d

pos *

*

pJMAA ) para calcular el parámetro J correspondiente a cada posición

M= (

pos p

d pos

pos experimental;

*

d) estimar los errores sistemáticos cometidos en los parámetros J calculados para cada posición,

pos realizar ajustes lineales con los pares de puntos (M (AA , Mp obtenidos modificando los p d ) )

pos *

parámetros por separado y tomar como error sistemático la máxima diferencia del valor de J

pos calculado anteriormente con los valores obtenidos con cada parámetro por separado; e) calcular el valor experimental para la reactividad del sistema pexp y su error mediante la expresión *

p =p J + ( (AA ) - (AA ) ) .

exp 0 pos p

dp

d

pos, exp

pos, 0

3. Procedimiento para la determinación de la constante de criticidad (keff) de un reactor nuclear subcrítico según la reivindicación 1 donde el estimador es la constante de decaimiento de los neutrones inmediatos (a) ,

obtenida mediante el ajuste a una exponencial de la curva de decaimiento de los neutrones inmediatos tras un pulso de la fuente, procedimiento que comprende los siguientes pasos:

a) para cada uno de los modelos definidos en f, calcular con el código de simulación los valores de la reactividad py la constante de decaimiento apos para cada una de las posiciones de los detectores;

b) para cada posición experimental, representar los valores así obtenidos de M= ppp frente a los valores de Ma =a-a ;

pos pos pos, 0 c) realizar un ajuste lineal por el método de los mínimos cuadrados de los pares de puntos (Mapos , Mp)

* *

a la expresión Mp=A Ma para calcular el parámetro A correspondiente a cada posición pos pos pos experimental;

*

d) estimar los errores sistemáticos cometidos en los parámetros A calculados para cada posición pos realizando tres ajustes lineales con los pares de puntos (Ma , Mp) obtenidos modificando los pos

*

parámetros por separado y tomar como error sistemático la máxima diferencia del valor de A

pos calculado anteriormente con los valores obtenidos con cada parámetro por separado;

e) calcular el valor experimental para la reactividad del sistema pexp y su error mediante la expresión * pexp =p0 +Apos (apos, exp -apos, 0 ) .

4. Procedimiento según cualquiera de las reivindicaciones anteriores caracterizado porque el código de simulación es MCNP.

5. Procedimiento según cualquiera de las reivindicaciones anteriores caracterizado porque los parámetros en el paso

f. son la densidad del moderador del reactor, la relación de aspecto del reactor y el enriquecimiento del combustible.