METODO PARA EL DISEÑO DE UN ECUALIZADOR MODAL PARA UNA GAMA AUDIBLE DE FRECUENCIAS BAJAS, ESPECIALMENTE PARA MODOS POSICIONADOS MUY PROXIMOS.

Método para la formación de un ecualizador modal (5) para una gama audible de frecuencias bajas,

en particular para frecuencias por debajo de los 200 Hz para un espacio (1) predeterminado y una ubicación (2) en el mismo, que comprende las etapas de:

- determinar los modos que se van a ecualizar al menos mediante una frecuencia central y una tasa de amortiguación de cada modo,

- crear una descripción en tiempo discreto de los modos determinados, y

- determinar los coeficientes del filtro ecualizador en base a la descripción en tiempo discreto de los modos determinados, y

- formar el ecualizador (5) mediante un filtro digital definiendo los coeficientes del filtro en base a las propiedades de los modos, en el que dicho método está caracterizado por las etapas de

- formar una función de detección de modo (G(omega)),

- definir la frecuencia omega p angular del pico más alto de la función (G(omega)),

- realizar un análisis autorregresivo de orden predefinido sobre la versión de fase mínima de la respuesta objetivo para resolver los polos del modo que representa la frecuencia angular del pico más elevado,

- seleccionar el polo más cercano al punto e j omega p del círculo unidad, para representar con su complejo conjugado el modo más importante,

- determinar el tiempo de amortiguación de dicho modo y si es superior a un nivel predeterminado, diseñar un filtro de corrección modal para dicho modo y aplicar dicho filtro de corrección modal a la respuesta que se va a ecualizar, y

- repetir este procedimiento hasta que ningún tiempo de amortiguación supere el nivel predeterminado y

- formar el ecualizador combinando todos los filtros de corrección modal obtenidos de esta manera en un filtro de ecualización modal en cascada

Método para el diseño de un ecualizador modal para una gama audible de frecuencias bajas, especialmente para modos posicionados muy próximos.

La presente invención se refiere a un método, de acuerdo con el preámbulo de la reivindicación 1, para formar un ecualizador modal para una gama audible de bajas frecuencias, especialmente para modos posicionados muy próximas.

El análisis y modelado paramétrico es una tarea cada vez más común en los campos de acústica y audio. En esta solicitud de patente nos centraremos en dichos problemas relacionados con el audio en los que se puede medir una respuesta de sistema objetivo y la tarea es modelarlo para una síntesis/simulación informática o para realizar un modelo inverso para su ecualización, es decir, compensar la falta de idealidad en la respuesta observada. Los ejemplos representativos del primer grupo, simulación directa para la síntesis, son el modelado de una respuesta de una sala que comprende el diseño de una reverberación artificial, o simplemente una estimación de los modos propios en bajas frecuencias en estudios acústicos de espacios cerrados, y el modelado de instrumentos musicales. La segunda categoría, el modelado inverso, es común en audio, donde la ecualización de las propiedades no ideales de la respuesta es una tarea frecuente en la reproducción de sonido de alta calidad, así como para evitar la realimentación acústica en los sistemas de refuerzo de sonido.

El comportamiento de los sistemas acústicos o de audio a bajas frecuencias se puede modelar a menudo de manera analítica y puede ser parametrizado, al menos con modelos concentrados, por ejemplo el comportamiento modal a bajas frecuencias de una sala rectangular [1], el cuerpo de un instrumento musical [2], o una envolvente de un altavoz [3]. Para estructuras irregulares y/o frecuencias más altas es más difícil o imposible encontrar modelos numéricos o analíticos que sean útiles en la práctica. En estos casos aún es posible medir las respuestas del sistema y aplicar técnicas de modelado de señales para analizar, simular o sintetizar en tiempo real una respuesta dada.

Un interés particular de este estudio se centra en las características de resonancia y reverberación de sistemas acústicos complejos. El comportamiento modal, es decir, la descomposición de los modos propios suponiendo un sistema lineal e invariante en el tiempo (LTI), puede ser extremadamente complicado. En resonadores unidimensionales, tales como cuerdas y tubos de instrumentos musicales, la densidad de los modos propios no es necesariamente alta, pero estos modos pueden presentar detalles complicados, por ejemplo, una amortiguación en dos etapas y una fuerte pulsación en una envolvente amortiguada. En resonadores de dos y tres dimensiones, tales como membranas, placas y espacios cerrados, la densidad modal aumenta hacia las frecuencias más altas, dando como resultado unas configuraciones modales densas y un comportamiento de tipo reverberativo cuando los modos propios adyacentes se superponen esencialmente. Además, el comportamiento temporal se vuelve complejo, especialmente en salas donde al sonido directo y a las primeras reflexiones les sigue un aumento de la densidad de las reflexiones que dan como resultado una reverberación tardía. De esta manera, el problema de modelar las respuestas medidas puede beneficiarse de un punto de vista de modelado en tiempo-frecuencia en el que también se tienen en cuenta las propiedades de la percepción del auditorio.

Existe una amplia literatura sobre el modelado de señales de sistemas LTI [4, 5, 6, 7] en muchas ramas de la ingeniería, ciencias de sistemas y aplicaciones. Se encuentran disponibles herramientas de programación para el modelado, por ejemplo en MATLAB. En este documento se utilizan particularmente las funciones que se encuentran en el paquete de herramientas de procesamiento de señales [8]. Otro paquete de herramientas de MATLAB que es de interés es el paquete de herramientas de identificación de sistemas [9]. En este documento se supone que el sistema objetivo y el modelo deseado son, además de lineales e invariantes en el tiempo, también estables y causales. También se supone que la respuesta medida no está demasiado contaminada por ruido, de manera que la estimación de los parámetros modales del sistema es práctica para las aplicaciones que se tratan aquí. Posteriormente, se puede aproximar la respuesta de impulso medida h(n) mediante una expresión racional en el dominio de la transformada en Z mediante

que hace posible simular o sintetizar el sistema de manera eficiente mediante diversas implementaciones de filtros digitales [5, 10, 11] de la función de transferencia dada.

En esta solicitud de patente se tratarán únicamente representaciones en tiempo discreto para el procesamiento digital de señales. De esta manera, la manera más fácil de "modelar" una respuesta medida h(n) o su versión truncada/parcial es tratarla directamente como un filtro FIR

Para sistemas complejos, la longitud de una respuesta de impulso finito requerida para una representación adecuada puede ser demasiado larga, impidiendo implementaciones en tiempo real. Por otra parte, la reducción de la longitud del filtro reduce las capacidades de identificación de las propiedades de resonancia inherentes del sistema bajo estudio. Los filtros IIR para respuesta de impulso infinito se pueden presentar en dos formas: (a) modelos totalmente polares en los que el numerador de la ecuación (1) se reduce a un único coeficiente de ganancia b₀ o (b) modelos de polo nulo en los que tanto el numerador como el denominador son polinomios de Z no triviales.

En la ciencia de sistemas y en ingeniería, por ejemplo en la teoría de control de tareas de estimación e identificación, los términos autorregresivo (A), media móvil (MA) y media móvil autorregresiva (ARMA) han sido utilizados para procesos de modelado similares al modelado de filtros totalmente polares, FIR, y de polo nulo, respectivamente. Por motivos de una utilización adecuada de las abreviaturas AR y ARMA, así como para llamar la atención a los amplios conocimientos de otros diversos campos además del de procesamiento de señales de audio digitales, en este documento se aplican los términos MA, AR y ARMA cuando se refieren a tipos de modelos específicos.

Nuestra intención no es limitarse a obtener una aproximación útil de un sistema objetivo medido mediante una función de transferencia de la ecuación [1]. Estamos interesados en descomponerla en una descripción paramétrica de sus componentes constitutivos, particularmente los pares de polos complejos conjugados, es decir, las raíces de valores complejos del polinomio del denominador, que representan los modos propios del sistema y dan como resultado el comportamiento resonante y reverberante. En teoría son comunes en sistemas distribuidos espacialmente tales como una sala [12] o el cuerpo de un instrumento, mientras que los ceros (raíces del numerador dependen esencialmente de la posición. Estamos interesados en una estimación precisa de los parámetros modales, tales como el ángulo polar y el radio o, de manera equivalente, la frecuencia del modo y el coeficiente de amortiguación.

En la ecuación [13] estudiamos este problema de la estimación de los parámetros modales utilizando las técnicas de análisis en tiempo-frecuencia tradicionales, intentando aislar, en primer lugar, las frecuencias de los modos potenciales y, posteriormente, estimando la tasa de amortiguación modal a partir de un espectrograma, tal como un análisis de Fourier de periodo corto o un espectro de amortiguación acumulativo [14]. La estimación de la tasa de amortiguación también fue aplicada a señales de banda ancha, por ejemplo para una estimación sólida del tiempo de reverberación T₆₀. El problema con dichos métodos es modelar modos superpuestos que dan como resultado una amortiguación no exponencial en cualquier intervalo de frecuencia razonable. Los enfoques AR y ARMA intentan modelar la respuesta objetivo en conjunto, minimizando un criterio de error de modelado dado, típicamente el error de mínimos cuadrados (LS). De esta manera, las interacciones de los modos superpuestos se tienen en cuenta simultánea y sistemáticamente.

Un problema de optimización directa...

1. Método para la formación de un ecualizador modal (5) para una gama audible de frecuencias bajas, en particular para frecuencias por debajo de los 200 Hz para un espacio (1) predeterminado y una ubicación (2) en el mismo, que comprende las etapas de:

- determinar los modos que se van a ecualizar al menos mediante una frecuencia central y una tasa de amortiguación de cada modo,

- crear una descripción en tiempo discreto de los modos determinados, y

- determinar los coeficientes del filtro ecualizador en base a la descripción en tiempo discreto de los modos determinados, y

- formar el ecualizador (5) mediante un filtro digital definiendo los coeficientes del filtro en base a las propiedades de los modos,

en el que dicho método está caracterizado por las etapas de

- formar una función de detección de modo (G(O)),

- definir la frecuencia Op angular del pico más alto de la función (G(O)),

- realizar un análisis autorregresivo de orden predefinido sobre la versión de fase mínima de la respuesta objetivo para resolver los polos del modo que representa la frecuencia angular del pico más elevado,

- seleccionar el polo más cercano al punto e^{jO p} del círculo unidad, para representar con su complejo conjugado el modo más importante,

- determinar el tiempo de amortiguación de dicho modo y si es superior a un nivel predeterminado, diseñar un filtro de corrección modal para dicho modo y aplicar dicho filtro de corrección modal a la respuesta que se va a ecualizar, y

- repetir este procedimiento hasta que ningún tiempo de amortiguación supere el nivel predeterminado y

- formar el ecualizador combinando todos los filtros de corrección modal obtenidos de esta manera en un filtro de ecualización modal en cascada.

2. Método, según la reivindicación 1, caracterizado porque la descripción en tiempo discreto es una transformada en Z.

3. Método, según la reivindicación 1 ó 2, caracterizado porque se aplica el orden 50-70 al análisis AR.

4. Método, según la reivindicación 1 ó 2 ó 3, caracterizado porque se utiliza un filtro de corrección de segundo orden de la ecuación

para corregir cada modo único.

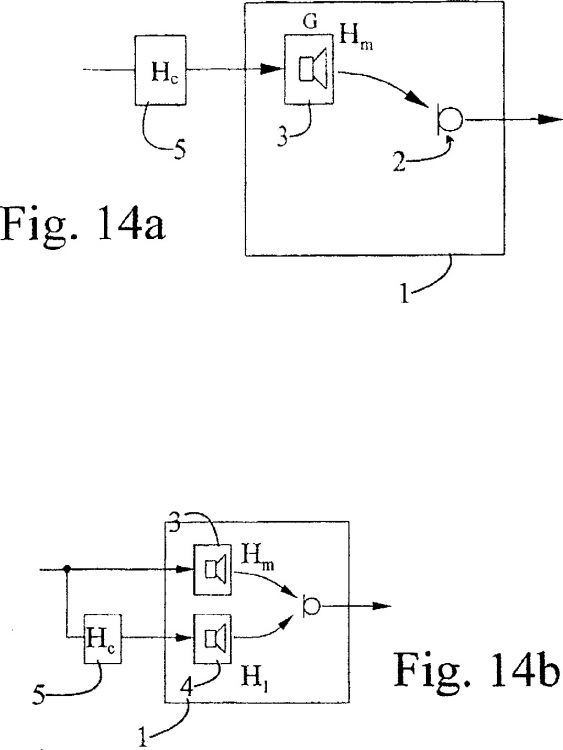
5. Método, según cualquiera de las reivindicaciones 1 a 4, caracterizado porque se modifica el sonido de los altavoces (3) principales.

6. Método, según cualquiera de las reivindicaciones 1 a 4, caracterizado porque se modifica el sonido de los altavoces (4) secundarios.