TABLERO GEONUMÉRICO.

1. Tablero geonumérico (1), caracterizado porque comprende

- un cuerpo cuadrangular (2) plano que comprende una serie de cuadrículas (3) numeradas consecutivamente y alineadas según dos direcciones perpendiculares;

- donde dentro de cada cuadrícula (3) se dispone de elementos de retención, y;

- unos medios de trazado de figuras geométricas que se colocan unidos a los elementos de retención e interactúan con la numeración de las cuadrículas (3).

2. Tablero geonumérico (1), según la reivindicación 1, caracterizado porque la numeración de las cuadrículas (3) comprende los números del 0 al 99.

3. Tablero geonumérico (1), según la reivindicación 1, caracterizado porque la numeración de las cuadrículas (3) comprende los números del 1 al 100.

4. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los elementos de retención están fijados al centro de la cuadrícula (3).

5. Tablero geonumérico (1), según la reivindicación 4, caracterizado porque los elementos de retención están formados por unos clavos (4) o elementos emergentes de las cuadrículas (3).

6. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los medios de trazado de figuras están formados por gomas (5) elásticas.

7. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los medios de trazado determinan al menos una forma de polígono regular, como un triángulo equilátero, cuadrado, pentágono, hexágono y cualquier otro con diferente número de lados.

8. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los medios de trazado determinan al menos una forma de polígono irregular, como un triángulo de lados de diferente longitud, un rectángulo, un rombo, un romboide, un trapecio, un trapezoide o cualquier otro con igual o diferente número de lados.

9. Tablero geonumérico (1), según cualquiera de las reivindicaciones 7 o/y 8, caracterizado porque los vértices del al menos un polígono interactúan con la numeración de las cuadrículas (3) del tablero en las que se encuentran, sobre las que se realiza alguna operación aritmética, como suma, resta, multiplicación o división.

10. Tablero geonumérico (1), según la reivindicación 9, caracterizado porque los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí a través de su interacción con la numeración de las cuadrículas (3) del tablero.

11. Tablero geonumérico (1), según cualquiera de las reivindicaciones 7 a 10, caracterizado porque los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí mediante una relación geométrica, como igualdad, semejanza, traslación, simetría, giro, equivalencia o cualquier otra.

12. Tablero geonumérico (1), según cualquiera de las reivindicaciones 7 a 11, caracterizado porque los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí mediante una relación aritmética.

Tablero geonumérico

Campo técnico de la invención 5

La presente invención corresponde al campo técnico de los recursos materiales y didácticos utilizados para la enseñanza de las matemáticas, en concreto de la geometría y la aritmética, en cursos de primaria y secundaria.

Antecedentes de la Invención

Las dificultades en la enseñanza y aprendizaje de la Geometría y la Aritmética siguen siendo objeto de preocupación y estudio en el ámbito de la educación en primaria y secundaria. De ahí la importancia de aportar materiales y recursos didácticos que faciliten la tarea de los 15 profesores y motiven al alumnado hacia su aprendizaje.

La geometría elemental trata el estudio de formas y medida en el plano y el espacio. Así analiza las propiedades de las diferentes figuras geométricas planas o espaciales. Por otra parte, la aritmética tiene como objeto el estudio de los números y las operaciones 20 elementales que, a su vez, son importantes en el desarrollo de la geometría.

Las matemáticas son una de las asignaturas fundamentales del currículo, presentando un elevado índice de fracaso escolar y desapego por un gran número de estudiantes. Consecuentemente, cualquier recurso que ayude y oriente a los alumnos y profesores en el 25 trabajo de esta materia es importante. Si además, puede hacerse de una forma lúdica, para que puedan aprenderse de manera amena y motivadora, resulta tremendamente interesante.

Descripción de la invención 30

El tablero geonumérico que aquí se propone, comprende un cuerpo cuadrangular plano que presenta una serie de cuadrículas numeradas consecutivamente y alineadas según dos direcciones perpendiculares, donde dentro de cada cuadrícula se dispone de elementos de retención y, unos medios de trazado de figuras geométricas que se colocan unidos a los 35 elementos de retención e interactúan con la numeración de las cuadrículas.

Según una realización preferida, la numeración de las cuadrículas comprende los números del 0 al 99.

Según otra realización preferente, la numeración de las cuadrículas comprende los números 5 del 1 al 100.

De acuerdo con otro aspecto, en una realización preferida, los elementos de retención están fijados al centro de la cuadrícula.

Según una realización preferente, los elementos de retención están formados por unos clavos o elementos emergentes de las cuadrículas.

De acuerdo con una realización preferente, los medios de trazado de figuras están formados por gomas elásticas. Estas gomas elásticas se utilizan de diferentes colores para una mejor 15 visualización de las figuras.

Según una realización preferente, los medios de trazado determinan al menos una forma de polígono regular, como un triángulo equilátero, cuadrado, pentágono, hexágono o cualquier otro con diferente número de lados. 20

Así mismo, en una realización preferida, los medios de trazado determinan al menos una forma de polígono irregular, como un triángulo de lados de diferente longitud, un rectángulo, un rombo, un romboide, un trapecio, un trapezoide o cualquier otro con igual o diferente número de lados. 25

Tanto en el caso en que los medios de trazado determinan al menos un polígono regular, como cuando determinan al menos un polígono irregular o bien ambos tipos de polígonos, de acuerdo con una realización preferente, los vértices del polígono interactúan con la numeración de las cuadrículas del tablero en las que se encuentran, sobre las que se realiza 30 alguna operación aritmética, como suma, resta, multiplicación o división.

En este caso y según una realización preferente, los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí a través de su interacción con la numeración de las cuadrículas del tablero. 35

Así mismo y de acuerdo con una realización preferente, los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí mediante una relación geométrica, como igualdad, semejanza, traslación, simetría, giro, equivalencia o cualquier otra en función de las propiedades geométricas.

Con el tablero geonumérico que aquí se propone se obtiene una mejora significativa del estado de la técnica.

Esto es así pues se consigue un tablero que permite combinar ambas materias, geometría y aritmética, para poder formular y resolver problemas de matemáticas, de una forma visual y 10 más sencilla para los alumnos.

Con este tablero es posible trabajar distintas figuras geométricas planas, en relación con su forma y propiedades y al mismo tiempo, trabajarlas desde la aritmética, considerando operaciones aritméticas y las propiedades del sistema de numeración, a través del valor 15 numérico de los vértices de dichas figuras geométricas.

Es posible por tanto, trabajar ciertos problemas interesantes y motivadores para los alumnos, que relacionan conceptos y procesos geométricos y aritméticos mediante un recurso completamente manipulativo y lúdico. 20

Resulta por tanto un recurso sencillo de utilizar y que gracias al modo de plantear y resolver problemas, tan práctico, intuitivo e instructivo, resulta muy interesante, motivador y eficaz en la enseñanza de estas materias a alumnos de primaria y secundaria.

Breve descripción de los dibujos

Con objeto de ayudar a una mejor comprensión de las características del invento, de acuerdo con un ejemplo preferente de realización práctica del mismo, se aporta como parte integrante de dicha descripción, una serie de dibujos donde, con carácter ilustrativo y no 30 limitativo, se ha representado lo siguiente:

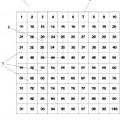
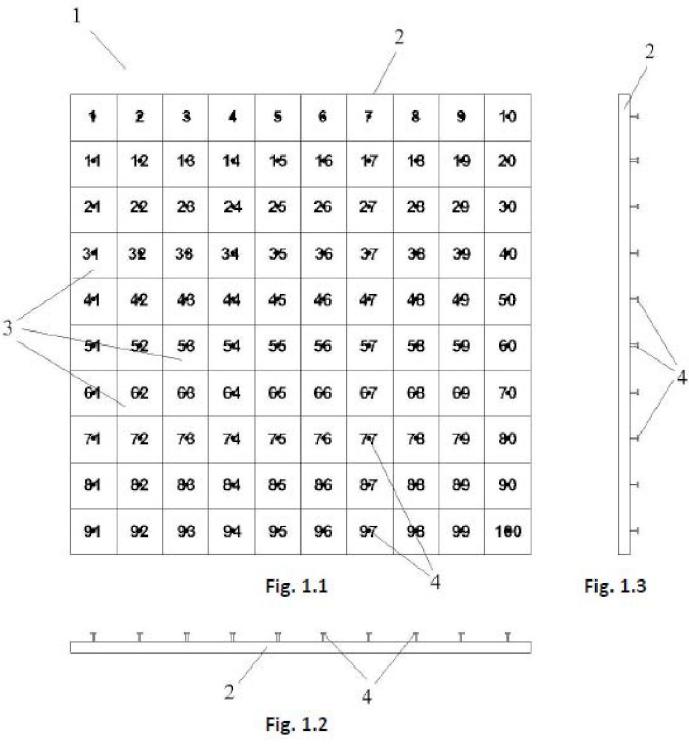
Las Figuras 1.1, 1.2 y 1.3. Muestran unas vistas en planta, alzado y perfil respectivamente, del tablero geonumérico, para un modo de realización preferente de la invención.

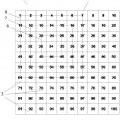
La Figura 2. Muestra una vista en planta del tablero geonumérico con la resolución de un primer problema planteado, para un modo de realización preferente de la invención.

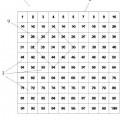
La Figura 3. Muestra una vista en planta del tablero geonumérico con la resolución de un segundo problema planteado, para un modo de realización preferente de la invención.

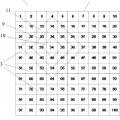
La Figura 4. Muestra una vista en planta del tablero geonumérico con la resolución de un 5 tercer problema planteado, para un modo de realización preferente de la invención.

La Figura 5. Muestra una vista en planta del tablero geonumérico con la resolución de un cuarto problema planteado, para un modo de realización preferente de la invención.

La Figura 6. Muestra una vista en planta del tablero geonumérico con la resolución de un quinto problema planteado, para un modo de realización preferente de la invención.

Descripción detallada de un modo de realización preferente de la invención 15

A la vista de las figuras aportadas, puede observarse cómo en un modo de realización preferente de la invención, el tablero geonumérico 1 que aquí se propone, comprende un cuerpo cuadrangular 2 plano que comprende una serie de cuadrículas 3 numeradas consecutivamente y alineadas según dos direcciones perpendiculares, disponiendo cada una de estas cuadrículas 3 de elementos de retención en su interior. El tablero geonumérico 20 1 comprende a su vez de unos medios de trazado de figuras geométricas que se colocan unidos a los elementos de retención e interactúan con la numeración de las cuadrículas 3.

Como se muestra en la Figura 1.1, en este modo de realización preferente de la invención, la numeración de las cuadrículas 3 comprende los números del 1 al 100. 25

Así mismo, como puede observarse en las Figuras 1.2 y 1.3, en este modo de realización preferente de la invención, los elementos de retención están formados por unos clavos 4 fijados al centro de la cuadrícula 3.

En este modo de realización preferente de la invención, los medios de trazado de figuras están formados por gomas 5 elásticas de colores. Estas gomas 5 son de diferente color, para poder diferenciar cada una de las figuras geométricas que se realizan en función de los problemas planteados.

En este modo de realización preferente de la invención, se puede plantear un primer problema consistente en definir mediante los medios de trazado, un polígono regular, como puede ser un triángulo o un cuadrado, de tal manera que la suma de sus vértices sea 136.

Así pues, en este caso se elige como figura geométrica un cuadrado y en la Figura 2 se 5 muestra la resolución a un posible primer problema consistente en construir, con las gomas 5 elásticas, un cuadrado 6, alrededor del número 34 del tablero, de tal manera...

1. Tablero geonumérico (1), caracterizado porque comprende

- un cuerpo cuadrangular (2) plano que comprende una serie de cuadrículas (3) numeradas consecutivamente y alineadas según dos direcciones perpendiculares;

- donde dentro de cada cuadrícula (3) se dispone de elementos de retención, y;

- unos medios de trazado de figuras geométricas que se colocan unidos a los elementos de retención e interactúan con la numeración de las cuadrículas (3).

2. Tablero geonumérico (1), según la reivindicación 1, caracterizado porque la numeración de las cuadrículas (3) comprende los números del 0 al 99.

3. Tablero geonumérico (1), según la reivindicación 1, caracterizado porque la numeración de las cuadrículas (3) comprende los números del 1 al 100.

4. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los elementos de retención están fijados al centro de la cuadrícula (3).

5. Tablero geonumérico (1), según la reivindicación 4, caracterizado porque los elementos de retención están formados por unos clavos (4) o elementos emergentes de las cuadrículas (3).

6. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los medios de trazado de figuras están formados por gomas (5) elásticas.

7. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los medios de trazado determinan al menos una forma de polígono regular, como un triángulo equilátero, cuadrado, pentágono, hexágono y cualquier otro con diferente número de lados.

8. Tablero geonumérico (1), según cualquiera de las reivindicaciones anteriores, caracterizado porque los medios de trazado determinan al menos una forma de polígono irregular, como un triángulo de lados de diferente longitud, un rectángulo, un rombo, un romboide, un trapecio, un trapezoide o cualquier otro con igual o diferente número de lados.

9. Tablero geonumérico (1), según cualquiera de las reivindicaciones 7 o/y 8, caracterizado porque los vértices del al menos un polígono interactúan con la numeración de las cuadrículas (3) del tablero en las que se encuentran, sobre las que se realiza alguna operación aritmética, como suma, resta, multiplicación o división.

10. Tablero geonumérico (1), según la reivindicación 9, caracterizado porque los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí a través de su interacción con la numeración de las cuadrículas (3) del tablero.

11. Tablero geonumérico (1), según cualquiera de las reivindicaciones 7 a 10, caracterizado porque los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí mediante una relación geométrica, como igualdad, semejanza, traslación, simetría, giro, equivalencia o cualquier otra.

12. Tablero geonumérico (1), según cualquiera de las reivindicaciones 7 a 11, caracterizado porque los medios de trazado determinan al menos dos figuras geométricas estando dichas figuras relacionadas entre sí mediante una relación aritmética.