Procedimiento y dispositivo de codificación y descodificación aritméticas de estados binarios y programa informático correspondiente y soporte de almacenamiento correspondiente legible por ordenador.

Un procedimiento para codificar aritméticamente un símbolo que hay que codificar que tiene un estado binariobasado en una anchura de intervalo actual R y representando una probabilidad una estimación de probabilidad parael símbolo que hay que codificar,

en el que la probabilidad está representada por un índice de probabilidad paraasignar un estado de probabilidad entre una pluralidad de estados de probabilidad representativos, en el que elprocedimiento comprende la siguiente etapa caracterizadora:

codificar el símbolo que hay que codificar realizando las siguientes sub-etapas:

cartografiar la anchura de intervalo actual con un índice de cuantización de entre una pluralidad de índices decuantización representativos;

realizar la subdivisión de intervalo mediante el acceso a una tabla de división de intervalo utilizando el índice decuantización y el índice de probabilidad para obtener un valor de la anchura de intervalo parcial;

actualizar la anchura de intervalo actual utilizando el valor de la anchura de intervalo parcial para obtener una nuevay actualizada anchura de intervalo; y

renormalizar la nueva y actualizada anchura de intervalo, dando como salida un bit por operación deescalonamiento.

Procedimiento y dispositivo de codificación y descodificación aritméticas de estados binarios y programa informático correspondiente y soporte de almacenamiento correspondiente legible por ordenador

La invención se refiere a un procedimiento y a un dispositivo para codificar aritméticamente y descodificar estados binarios y a un programa informático correspondiente y un medio de almacenamiento legible por ordenador correspondiente que puede en particular ser utilizado en la compresión de datos digitales.

La presente invención describe un nuevo procedimiento eficiente para la codificación aritmética binaria. Existe una demanda para la codificación aritmética binaria en la mayoría de áreas de aplicación diferentes de compresión de datos digitales; aquí, en particular, son especialmente interesantes las aplicaciones en los sectores de la compresión de imágenes digitales. En numerosas normas para la codificación de imágenes, como por ejemplo, JPEG, JPEG -2000, JPEG -LS y JPIG, se definieron procedimientos para una codificación aritmética binaria. Las actividades de normalización más nuevas también prevén de manera obvia el uso futuro de estas tecnologías de codificación en el campo de la codificación video (CABAC en H. 264/AVC) [1].

Las ventajas de la codificación aritmética (CA) en contraste con la codificación de Huffman [2] que hasta ahora se había utilizado en la práctica, se pueden caracterizar básicamente por tres características:

1. Mediante el uso de la codificación aritmética, por mecanismos de adaptación simples se puede obtener una adaptación dinámica a la presente estadística de fuente (adaptabilidad) .

2. La codificación aritmética permite la asignación de un número de bits no entero por símbolo que va a codificarse y es por lo tanto adecuada para lograr resultados de codificación que ilustran una aproximación de la entropía como límite inferior dado teóricamente (aproximación de entropía) [3].

3. Se pueden utilizar enlaces estadísticas de modelos de contexto adecuados entre símbolos para una reducción adicional de datos con la codificación aritmética (redundancia entre símbolos) [4].

Como desventaja de una aplicación de la codificación aritmética, se considera en general el aumento del esfuerzo de cálculo en comparación con la codificación de Huffman.

El concepto de la codificación aritmética se remonta a la documentación básica para la teoría de información por Shannon [5]. Los primeros procedimientos de construcción conceptuales fueron publicados primeramente por Elias [6]. Una primera variante LIFO (last-in-first-out) de la codificación aritmética fue diseñada por Rissanen [7] y más tarde modificada [8] [9] [10] por diferentes autores de las implementaciones FIFO (first-in-first-out) .

Todos estos documentos tienen como principio básico común la descomposición de intervalo parcial recursiva. En correspondencia con las probabilidades dadas P (“0”) y P (“1”) de dos resultados {“0”, “1”} de un alfabeto binario un intervalo dado principalmente, por ejemplo el intervalo [0, 1) , se descompone de forma recursiva en intervalos parciales dependiendo de la ocurrencia de eventos individuales. Aquí, el tamaño del intervalo parcial resultante como el producto de las probabilidades individuales de los eventos que ocurren es proporcional a la probabilidad de la secuencia de eventos individuales. Como cada evento Si añade una contribución de H (Si) = log (P (Si) ) del contenido de información teórica H (Si) de Si a la tasa global por la probabilidad P (Si) , una relación entre el número NBit de bits para ilustrar el intervalo parcial y la entropía de la secuencia de los resultados de los eventos individuales, que viene dada por el término derecho de la ecuación siguiente:

NBIi =− log∏I P (SI) = −II logP (SI)

El principio básico, sin embargo, requiere en primer lugar de una precisión ilimitada (teóricamente) en la ilustración del intervalo parcial resultante y aparte de esto, tiene la desventaja de que sólo después de la codificación de los últimos resultados pueden darse como salida los bits para una representación de intervalo parcial resultante. A los efectos de aplicación práctica, fue decisivo por lo tanto desarrollar mecanismos para una salida gradual de bits con una representación simultánea con números con una precisión fija predeterminada. Estos mecanismos se introdujeron por primera vez en los documentos [3] [7] [11].

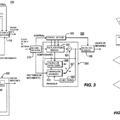
En la figura 1, se indican las operaciones básicas para una codificación aritmética binaria. En la implementación ilustrada el intervalo parcial actual está representado por los dos valores L y R, donde L indica el punto de desplazamiento y R el tamaño (anchura) del intervalo parcial, donde ambas cantidades se ilustran, utilizando números b bits enteros respectivamente. La codificación de un bit ∈ {0, 1} se lleva a cabo de este modo, básicamente, en cinco subetapas: En la primera etapa se determina el valor del símbolo menos probable utilizando la estimación de probabilidad. Para este símbolo, también llamado LPS (Least Probable Symbol- símbolo menos probable) , en contraste con el MPS (Most Probable Symbol- símbolo más probable) , se utiliza la estimación de probabilidad PLPS en la segunda etapa para calcular la anchura RLPS del intervalo parcial correspondiente. Dependiendo del valor del bit que hay que codificar L y R se actualizan en la tercera etapa. En la cuarta etapa se actualiza la estimación de probabilidad en función del valor del bit que se acaba de codificar y finalmente el intervalo de código R se somete a la así llamada renormalización en la última etapa, es decir R se reescala por ejemplo para que se satisfaga la condición R∈[2b-2, 2b-1]. Aquí, se da como salida un bit en cada operación de escalado. Para más detalles, consulte [10].

La principal desventaja de una implementación, tal como se indica más arriba, reside ahora en el hecho de que el cálculo de la anchura de intervalo RLPS requiere una multiplicación para cada símbolo que hay que codificar. En general, las operaciones de multiplicación, en particular cuando se realizan en hardware, son costosas y requieren mucho tiempo. En varios documentos de investigación se examinaron los procedimientos para sustituir esta operación de multiplicación por una aproximación adecuada [11] [12] [13] [14]. Por la presente, los procedimientos publicados con referencia a este tema se pueden separar generalmente en tres categorías.

El primer grupo de propuestas para una codificación aritmética binaria libre de multiplicaciones, se basa en el enfoque de la aproximación de las probabilidades estimadas PLPS para que la multiplicación en la segunda etapa de La figura 1 podrá sustituirse por una o varias operaciones de suma y desplazamiento [11] [14]. Para esto, en el caso más simple las probabilidades PLPS se aproximan por valores en la forma 2-q con el entero q > 0.

En la segunda categoría de procedimientos aproximativos se propone aproximar el rango de valores de R por valores discretos en la forma (1/2 – r) , donde se selecciona r ∈ {0} ∪ {2-k I k > 0, k entero} [15] [16].

La tercera categoría de procedimientos sólo se conoce por el hecho de que aquí cualquier operación aritmética se sustituye por accesos a tabla. La tercera categoría de procedimientos sólo se conoce por el hecho de que aquí cualquier operación aritmética se sustituye por accesos a tabla. A este grupo de procedimientos pertenecen, por un lado el codificador Q utilizado en los procedimientos JPEG estándar y los relacionados, tales como los codificadores QM - y MQ - [12], y por otro lado el codificador cuasi aritmético [13]. Mientras que este último procedimiento realiza una limitación drástica del número b de bits utilizados para la representación de R con el fin de obtener tablas aceptablemente dimensionadas, en el codificador Q la renormalización de R se implementa de manera que R puede al menos aproximadamente ser aproximado por 1. De esta manera se evita la multiplicación para determinar RLPS. Además, se realiza la estimación de probabilidad mediante una tabla en la forma de una máquina de estado finito. Además, se realiza la estimación de probabilidad mediante una tabla en la forma de una máquina de estado finito [12].

El documento de patente US5592162 describe un procedimiento de realización de codificación aritmética, estando el número de posibles intervalos de anchuras restringido.

Mediante el uso de un índice relativo a dichas anchuras de intervalo, la codificación aritmética libre de multiplicaciones se puede lograr con una sobrecarga... [Seguir leyendo]

1. Un procedimiento para codificar aritméticamente un símbolo que hay que codificar que tiene un estado binario basado en una anchura de intervalo actual R y representando una probabilidad una estimación de probabilidad para el símbolo que hay que codificar, en el que la probabilidad está representada por un índice de probabilidad para asignar un estado de probabilidad entre una pluralidad de estados de probabilidad representativos, en el que el procedimiento comprende la siguiente etapa caracterizadora:

codificar el símbolo que hay que codificar realizando las siguientes sub-etapas:

cartografiar la anchura de intervalo actual con un índice de cuantización de entre una pluralidad de índices de cuantización representativos;

realizar la subdivisión de intervalo mediante el acceso a una tabla de división de intervalo utilizando el índice de 15 cuantización y el índice de probabilidad para obtener un valor de la anchura de intervalo parcial;

actualizar la anchura de intervalo actual utilizando el valor de la anchura de intervalo parcial para obtener una nueva y actualizada anchura de intervalo; y

renormalizar la nueva y actualizada anchura de intervalo, dando como salida un bit por operación de escalonamiento.

2. Un procedimiento para descodificar aritméticamente un símbolo codificado que tiene un estado binario basado en una anchura de intervalo actual R y representando una probabilidad una estimación de probabilidad para el símbolo codificado, en el que la probabilidad está representada por un índice de probabilidad de un estado de probabilidad entre una pluralidad de estados de probabilidad representativos, en el que el procedimiento comprende la siguiente etapa caracterizadora:

descodificar el símbolo codificado realizando las siguientes sub-etapas:

cartografiar la anchura de intervalo actual con un índice de cuantización de entre una pluralidad de índices de cuantización representativos;

realizar la división de intervalo mediante el acceso a una tabla de división de intervalo utilizando el índice de 35 cuantización y el índice de probabilidad para obtener un valor de la anchura de intervalo parcial;

actualizar la anchura de intervalo actual utilizando el valor de la anchura de intervalo parcial y un valor dentro de un intervalo parcial para obtener una nueva y actualizada anchura de intervalo; y

renormalizar la nueva anchura de intervalo actualizada y, con cada bit leído, refinar gradualmente el valor dentro del intervalo parcial.

3. Un programa de ordenador que permite a un ordenador tras haber sido cargado en la memoria del ordenador realizar un procedimiento según la reivindicación 1 o la 2.

4. Un medio de almacenamiento legible por ordenador en el que hay un programa almacenado que permite a un ordenador tras haber sido cargado en la memoria del ordenador realizar un procedimiento según la reivindicación 1

o la 2.

1. Determinación del LPS

2. Cálculo de las variables RLPS y RMPS:

RLPS = R X RLPS

RMPS = R – RLPS

3. Cálculo del nuevo intervalo parcial:

if (bit: LPS) then L L + RMPS R RLPS

else R RMPS

4. Actualización de la estimación de probabilidad PLPS

5. Dar como salida los bits y renormalizar R

Fig.1

1. Determinación del LPS

2. Cuantización de R:

q_index = Qtab[R>>q]

3. Determinación de RLPS y RMPS:

RLPS = Rtab [q_index, p_state] RMPS = R – RLPS

4. Cálculo del nuevo intervalo parcial:

if (bit: LPS) then L L + RMPS

R RLPS

p_state Next_State_LPS [p_state]

else

R RMPS

p_state Next_State_MPS [p_state]

Fig.2

1. Determinación del LPS

2. Cuantización de R:

q_index = Qtab[R>>q]

3. Determinación de RLPS y RMPS:

RLPS = Rtab [q_index, p_state] R = R – RLPS

4. Determinación de bit en función de la posición del intervalo parcial:

if (V ≥ RMPS) then

bit LPS

V V -RMPS

R RLPS

p_state Next_State_LPS [p_state]

else bit MPS R RMPS p_state Next_State_MPS [p_state]

5. Renormalización de R, leer un bit y actualizar V

Fig.3

Codificador:

1. Cálculo del nuevo intervalo parcial

R R >> 1

if (bit = 1) then

L L + R

2. Dar como salida los bits y renormalizar R

Descodificador:

1. Determinación de bit en función de la posición del intervalo parcial:

if (V ≥ R) then

bit 1

V V – R

else bit 0,

2. Leer un bit, renormalizar R y actualizar V

Fig.4

Codificador:

1. Cálculo del nuevo intervalo parcial

L L << 1

if (bit = 1) then

L L + R

2. Dar como salida un bit y renormalizar utilizando valores umbrales de determinación duplicados (sin duplicar R y L)

Descodificador:

1. Leer un bit y actualizar V

2. Determinación de bit en función de la posición del intervalo parcial:

if (V ≥ R) then

bit 1

V V – R

else

Fig.5

1. preState = min (max (1, ( (m * SliceQP) >>4) +n) , 126)

2. if (preState <=63) then p_state = 63 – preState valMPS = 0

else p_state = preState – 64 valMPS = 1,

Fig.6