Cálculo del inverso modular de un valor.

Procedimiento implementado por ordenador para la determinación de pares de claves en un procedimiento de firma o de codificación RSA mediante el cálculo del inverso (R) modular de un valor (E) respecto a un módulo (M) mediante las siguientes etapas:

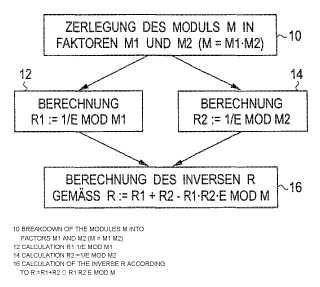
a) determinar (10) una descomposición del módulo (M) en al menos dos factores P-1 y Q-1, siendo P y Q los números primos preestablecidos en RSA,

b) calcular (12, 14) en cada caso un valor (R1, R2) auxiliar para cada uno de los factores (P-1, Q-1) determinados en la etapa a), siendo cada valor (R1, R2) auxiliar el inverso modular del valor (E) respecto al factor (P-1, Q-1) respectivo como módulo, y

c) calcular (16) el inverso (R) modular del valor (E) respecto al módulo (M) al menos empleando los valores (R1, R2) auxiliares calculados en la etapa b) .

Cálculo del inverso modular de un valor.

La invención se refiere en general al campo técnico de los algoritmos ejecutables de manera eficaz mediante un procesador automático y en especial a un algoritmo mejorado para la inversión modular. En particular la invención es adecuada para aplicaciones criptográficas, tal como aparecen, por ejemplo, en relación con tarjetas con circuito integrado.

En el campo de la criptografía se utilizan procedimientos para la inversión modular por ejemplo, en la generación de un par de claves para el procedimiento de firma y de codificación RSA descrito en la patente US 4.405.829. El procedimiento RSA emplea una clave (E, N) pública y una clave R privada secreta, siendo el valor N el producto de dos números P y Q primos grandes. Para el cálculo de pares de claves se fijan en primer lugar los valores P, Q y E. La clave R privada se calcula entonces como el inverso modular del valor E respecto al módulo M con M = (P-1) · (Q-1) .

En general para dos números E y M enteros dados el inverso modular del valor E respecto al módulo M está definido como aquel número R, para el que se cumple que 0 : R < M Y 1 = E·R mod M; el resultado R se designa también con 1/E. Un inverso R modular existe, cuando E y M son primos entre sí.

Se conocen como tales algoritmos para el cálculo del inverso modular de un valor E preestablecido respecto a un módulo M preestablecido. Así por ejemplo, se describe el empleo del algoritmo de Euclides ampliado para la inversión modular en las páginas 47 y 67 del libro de J. v. z. Gathen y J. Gerhard, “Modern Computer Algebra”, 1ª edición, Cambridge University Press, 1999 (algoritmo 3.6 y teorema 4.1) . Un pequeño aumento de la eficiencia en el ejemplo de aplicación del cálculo de pares de claves RSA es posible mediante una transformación según el teorema chino del resto. Una modificación ventajosa del algoritmo de Euclides ampliado en particular en relación con números binarios es el procedimiento de Stein, que se describe en las páginas 321 a 324 del libro de Donald E. Knuth, “The Art of Computer Programming”, tomo 2, 2ª edición, Addison-Wesley, 1981 en relación con el problema 35 de la página 339 y la solución para el mismo en la página 606.

Los procedimientos mencionados para la inversión modular requieren sin embargo relativamente mucho esfuerzo de cálculo. Necesitan un múltiplo del tiempo de cálculo de otras operaciones de cálculo modulares elementales tales como, por ejemplo, de la multiplicación modular (véase la página 304, corolario 11.6 del libro mencionado de Gathen y Gerhard) . Esto es especialmente problemático, cuando la inversión modular debe realizarse por un procesador con una capacidad de potencia relativamente reducida, como se produce por ejemplo, en el caso del procesador de una tarjeta con circuito integrado u otro soporte informático portátil.

La invención tiene por tanto el objetivo de proporcionar un procedimiento eficaz en la ejecución a máquina para la inversión modular. El procedimiento debe ser adecuado en particular para su empleo para cálculos criptográficos en un soporte informático portátil.

Según la invención este objetivo se soluciona parcial o totalmente mediante un procedimiento con las características de la reivindicación 1, un producto de programa informático según la reivindicación 9 y un soporte informático portátil según la reivindicación 10. Las reivindicaciones dependientes definen configuraciones preferidas de la invención.

La invención parte de la reflexión básica de que el esfuerzo para el cálculo del inverso modular depende en gran parte de la longitud del módulo. La invención propone por tanto dividir el cálculo total en varios cálculos parciales, basados en cada caso en un módulo más corto. Más concretamente el módulo se descompone según la invención en al menos dos factores. Entonces para el cálculo de un valor auxiliar se recurre a cada uno de estos factores, que es el inverso modular del valor original respecto al factor como módulo. A partir de los valores auxiliares calculados y dado el caso de datos adicionales se determina entonces el resultado total.

La idea básica según la invención es sorprendente, porque en general la factorización de un valor, en este caso del módulo, va unida a esfuerzos prohibitivos. El inventor ha reconocido sin embargo, que en muchas situaciones relevantes de modo práctico ya se conoce una factorización al menos parcial del módulo o los factores pueden calcularse fácilmente a partir de otra información. Este es el caso, por ejemplo, en el cálculo de pares de claves descrito al principio para el procedimiento RSA, en el que los factores P-1 y Q-1 del módulo M están fácilmente a disposición.

La invención ofrece un aumento considerable de la eficiencia, que es mayor, cuanto mayor sea la dependencia del esfuerzo de cálculo de la longitud del módulo en el procedimiento de inversión empleado finalmente. Con ello la invención es especialmente adecuada para su realización mediante procesadores relativamente poco potentes. La seguridad del cálculo frente a ataques de espionaje no se ve perjudicada por la utilización de la invención, en comparación con los procedimientos de inversión habituales. Cuando existen requisitos de seguridad especialmente altos, la invención puede combinarse sin embargo fácilmente con medidas adecuadas para la protección frente al espionaje.

El orden de enumeración de las etapas del procedimiento en las reivindicaciones no debe entenderse como una limitación del alcance de la invención. Están previstas muchas más configuraciones de la invención, en las que estas etapas de procedimiento se ejecutan en otro orden y/o total o parcialmente paralelas y/o total o parcialmente entrelazadas entre sí (interleaved) . Además la invención no está limitada al tratamiento de número enteros. El procedimiento según la invención puede utilizarse más bien como valores por ejemplo polinomios o en general los elementos de un anillo conmutativo con elemento universal.

Según la invención está previsto determinar una descomposición factorial del módulo. El término “determinar” debe comprender a este respecto también casos, en los que solamente se accede a factores ya conocidos, preestablecidos. Cuando solamente se conocen dos factores, a este respecto no se realiza ningún tipo de selección. Si se conocen más factores, entonces se selecciona preferiblemente el número necesario de factores. A este respecto los factores pueden clasificarse según su longitud o tamaño o agruparse adecuadamente. Por el término “longitud” debe entenderse a este respecto en particular el número de las posiciones del factor en un sistema de notación posicional tal como por ejemplo el sistema binario o decimal.

Los factores no necesitan ser primos. Por los términos “factorización” o “descomposición” no debe entenderse por tanto necesariamente una descomposición de factores primos. En configuraciones preferidas de la invención está previsto más bien tratar también factores compuestos sin división adicional, cuando por ejemplo no se conoce una división tal o si condujera a factores de longitudes muy diferentes. Por motivos de eficacia es deseable, que las longitudes de los factores, a los que solamente se recurre como módulos para la determinación de inversos según un procedimiento conocido, se diferencien lo menos posible (por ejemplo en menos del 20% o en menos del 50% de la mayor longitud) .

Dado que en general la factorización de un valor requiere un extraordinario esfuerzo de cálculo, el procedimiento se utiliza preferiblemente sólo cuando se conocen al menos dos factores del módulo o pueden determinarse con poco esfuerzo. Un esfuerzo pequeño en este sentido se considera en particular cuando la descomposición factorial ya no requiere más operaciones de cálculo que la determinación de inversos del valor respecto al más largo de los factores determinados como módulo.

El procedimiento ya puede utilizarse de manera útil con una única división del módulo en dos o tres o más factores. Si se conocen más factores o pueden determinarse fácilmente, así el procedimiento puede ejecutarse repetidamente, siendo posible una programación recursiva o una iterativa. Preferiblemente el módulo M presenta factores primos diferentes o se descompone en al menos una etapa de cálculo en al menos dos factores diferentes.

El producto de programa informático según la invención... [Seguir leyendo]

1. Procedimiento implementado por ordenador para la determinación de pares de claves en un procedimiento de firma o de codificación RSA mediante el cálculo del inverso (R) modular de un valor (E) respecto a un módulo (M) mediante las siguientes etapas:

a) determinar (10) una descomposición del módulo (M) en al menos dos factores P-1 y Q-1, siendo P y Q los números primos preestablecidos en RSA, b) calcular (12, 14) en cada caso un valor (R1, R2) auxiliar para cada uno de los factores (P-1, Q-1) determinados en la etapa a) , siendo cada valor (R1, R2) auxiliar el inverso modular del valor (E) respecto al factor (P-1, Q-1) respectivo como módulo, y c) calcular (16) el inverso (R) modular del valor (E) respecto al módulo (M) al menos empleando los valores (R1, R2) auxiliares calculados en la etapa b) .

2. Procedimiento según la reivindicación 1, caracterizado porque en la etapa c) el inverso (R) modular del valor (E) respecto al módulo (M) se calcula según la relación

.

3. Procedimiento según la reivindicación 2, caracterizado porque en al menos un cálculo la relación (*) , dado el caso unida al cálculo del valor auxiliar, se valora repetidamente en un procedimiento iterativo.

4. Procedimiento según una de las reivindicaciones 1 ó 2, caracterizado porque en al menos un cálculo en la etapa b) se realiza una llamada recursiva del procedimiento.