PROCEDIMIENTO Y DISPOSITIVO DE REDUCCIÓN DE UN POLINOMIO EN UN CAMPO FINITO BINARIO, EN PARTICULAR PARA UNA APLICACIÓN CRIPTOGRÁFICA.
Procedimiento utilizable en un procedimiento criptográfico en un dispositivo electrónico para reducir una primera palabra de datos binaria,
que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1, a una segunda palabra de datos con una longitud máxima igual a m, que corresponde a un polinomio C''0(x) equivalente a C(x) en un campo finito binario GF(2m) cuyos elementos tienen una longitud máxima igual a m, siendo m menor o igual que n, que incluye los siguientes pasos: - preparación de un polinomio de reducción R(x) consistente en un trinomio o un pentanomio; - partición de la primera palabra de datos en una primera subpalabra de datos binaria C0 y una segunda subpalabra de datos binaria C1 cuyos polinomios correspondientes, C0(x) y C1(x), satisfacen la ecuación C(x)=C1(x)*xm+C0(x), y toma de la segunda subpalabra de datos para formar un primer término de sumandos; - desplazamiento a la derecha de la segunda subpalabra de datos para formar un segundo término de sumandos, y repetición del paso de desplazamiento a la derecha para formar otros términos de sumandos hasta que cada término que no desaparezca del polinomio de reducción, que no sea el término xm, tenga asignado un término de sumandos, siendo la anchura de paso de cada desplazamiento a la derecha igual a la diferencia entre m y el orden de un término correspondiente que no desaparece del polinomio de reducción; - adición de los términos de sumandos formados a la primera subpalabra de datos para formar una palabra de datos de suma; - si la palabra de datos de suma así determinada tiene una longitud mayor que m, aplicación de los pasos de procedimiento a partir del paso de partición a la palabra de datos de sumandos formada, hasta que la palabra de datos de suma así determinada tenga una longitud máxima igual a m y por consiguiente constituya la segunda palabra de datos
Tipo: Patente Internacional (Tratado de Cooperación de Patentes). Resumen de patente/invención. Número de Solicitud: PCT/EP2007/052707.
Solicitante: IHP GMBH-INNOVATIONS FOR HIGH PERFORMANCE MICROELECTRONICS / LEIBNIZ-INSTITUT FÜR INNOVATIVE MIKRO.
Nacionalidad solicitante: Alemania.
Dirección: IM TECHNOLOGIEPARK 25 15236 FRANKFURT / ODER ALEMANIA.
Inventor/es: LANGENDÖRFER,Peter, PETER,Steffen.
Fecha de Publicación: .
Fecha Solicitud PCT: 21 de Marzo de 2007.
Clasificación Internacional de Patentes:
- G06F7/72F
Clasificación PCT:
- G06F7/72 FISICA. › G06 CALCULO; CONTEO. › G06F PROCESAMIENTO ELECTRICO DE DATOS DIGITALES (sistemas de computadores basados en modelos de cálculo específicos G06N). › G06F 7/00 Métodos o disposiciones para el procesamiento de datos actuando sobre el orden o el contenido de los datos tratados (circuitos lógicos H03K 19/00). › que utilizan la aritmética de restos.
Países PCT: Austria, Bélgica, Suiza, Alemania, Dinamarca, España, Francia, Reino Unido, Grecia, Italia, Liechtensein, Luxemburgo, Países Bajos, Suecia, Mónaco, Portugal, Irlanda, Eslovenia, Finlandia, Rumania, Chipre, Lituania, Letonia.
PDF original: ES-2357290_T3.pdf

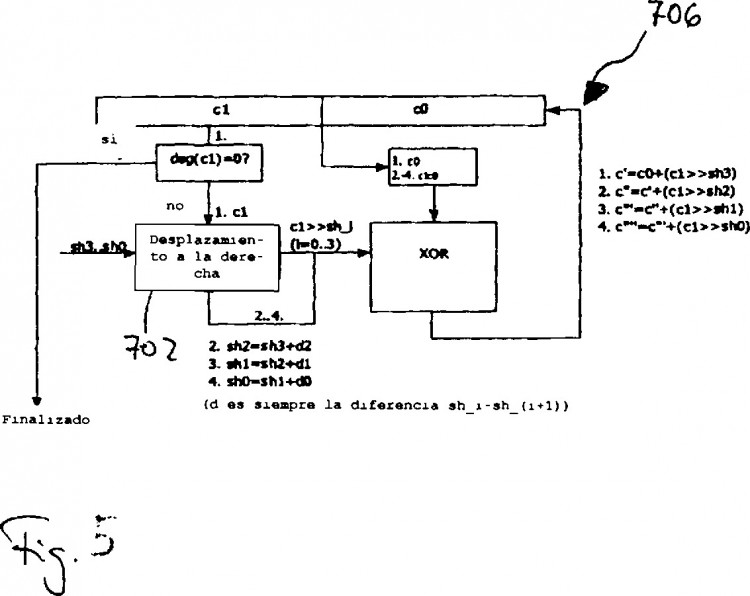
Fragmento de la descripción:
Procedimiento y dispositivo de reducción de un polinomio en un campo finito binario, en particular para una aplicación criptográfica.
La invención se refiere a un procedimiento y un dispositivo para reducir una primera palabra de datos binaria, que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1, a una segunda palabra de datos con una longitud máxima igual a m, que corresponde a un polinomio C''0(x) equivalente a C(x) en un campo finito binario cuyos elementos tienen una longitud máxima igual a m, siendo m menor o igual que n. La invención también se refiere a un procedimiento y un dispositivo criptográfico.
Los procedimientos criptográficos sirven para proteger datos frente a un acceso no autorizado. Los procedimientos criptográficos transforman los datos a proteger, en particular incluyendo un código secreto, en datos codificados. Los procedimientos criptográficos sirven también para descodificar los datos codificados incluyendo el código secreto para restablecer los datos a proteger.
Los procedimientos de codificación asimétricos como el RSA y la criptografía de curva elíptica (Elliptic Curve Cryptography, ECC) se utilizan para garantizar un intercambio seguro de códigos para procedimientos criptográficos y para calcular firmas digitales.
La criptografía de curva elíptica requiere una longitud de código claramente menor que el RSA con el mismo grado de seguridad. Además, para la criptografía de curva elíptica se pueden utilizar campos de Galois finitos binarios GF(2m), que gracias a sus propiedades algebraicas son muy adecuados para implementaciones de hardware. En este contexto, m indica la longitud de los elementos de cada campo de Galois correspondiente.
La operación más importante en la utilización de la criptografía de curva elíptica consiste en la multiplicación de grandes polinomios. Como es sabido, después de una multiplicación de polinomios en un campo finito, los posibles productos resultantes son más largos que el elemento más grande del campo finito utilizado como base. Por ello, después de una multiplicación de polinomios se ha de llevar a cabo una, así llamada, reducción. En esta reducción, el polinomio largo del producto resultante se convierte en un valor ("equivalente") dentro de los límites del campo. Esta operación es necesaria después de cada multiplicación de polinomios.
Dado que la multiplicación en la criptografía de curva elíptica constituye una operación principal, no sólo la operación de multiplicación es crítica para el rendimiento (performance) en el sentido de la rapidez de una implementación de ECC, sino también la operación de reducción.
La reducción corresponde a la división con resto (operación módulo) en campos finitos "normales". Esto se puede explicar mediante un sencillo ejemplo: el campo finito GF(7) consiste en los elementos {0,1,2,3,4,5,6}. Una multiplicación de 5*4 es igual a 20, que es mayor que el elemento más grande posible en el campo. En este caso se divide 20 por 7 y el resto de esta división, es decir, 6, es también el resultado de la multiplicación de 5*4 dentro del campo finito (GF(7)).
Los campos finitos binarios (GF(2m)) no incluyen números, sino polinomios. Un elemento de estos campos es A(x)=am-1*xm-1+am-2*xm-2+...+a1*x+a0. Los coeficientes ai son 0 o 1. Una propiedad importante de los campos consiste en que en la adición y sustracción de coeficientes se utiliza la operación XOR (O exclusiva). Por tanto, 1+1≡1-1≡1 XOR 1=0.
La longitud máxima de un elemento del campo GF(2m) es m. La multiplicación de dos elementos (A(x)*B(x)) da como resultado un polinomio el doble de largo C(x)=A(x)*B(x)=cm-2*x2m-2+...+c0. Por tanto, el resultado tiene una longitud de 2m-1.
El polinomio C(x) se puede descomponer en C(x)= C1(x)*xm+C0(x). C0(x) tiene la longitud correspondiente a la longitud máxima de los polinomios del campo. C1(x) es la parte que sobresale de la longitud máxima del campo y que se ha de integrar en C0 mediante el proceso de reducción.
Esta reducción puede resolverse mediante una división de polinomios completa, lo que requiere mucho tiempo. Un procedimiento de este tipo corresponde exactamente a la división módulo arriba explicada en el ejemplo de GF(7).
Existen posibilidades alternativas para realizar esta reducción más rápidamente. Un método usado con frecuencia consiste en la reducción multiplicativa. Si se multiplica C1(x) por un polinomio de reducción R(x) y el producto obtenido se le resta a C(x), el resultado es menor que el polinomio inicial, pero equivalente dentro del campo usado como base. Es aplicable: C(x)≡C(x)-C1(x)*R(x). Si se repite esta operación se obtienen campos cada vez más pequeños, pero equivalentes dentro del campo utilizado como base. La reducción termina cuando C1(x) llega a la longitud cero.
Si se conoce la longitud del campo y el polinomio de reducción R(x), se puede realizar muy eficientemente un cableado directo de la lógica de reducción. Esto se da a conocer p. ej. en la publicación de Saqib, N. A., Rodriguez-Henriquez, F., y Diaz-Perez, A., "A parallel architecture for fast computation of elliptic curve scalar multiplication over GF(2m)", 18th International Parallel & Distributed Processing Symposium (IPDPS), Santa Fe, New Mexico, 26-30 de abril de 2004.
Sin embargo, la desventaja del sistema dado a conocer en dicha publicación consiste precisamente en que requiere el conocimiento de la longitud del campo y del polinomio de reducción R(x). Por ello se intenta encontrar un método con una eficiencia similar que posibilite estas operaciones para campos de duración variable con polinomios de reducción variables en hardware.
Una posibilidad ya dada a conocer en el documento de Eberle, H., Gura, N., y Chang-Shantz, S., "A cryptograhpic processor for arbitrary elliptic curves over GF(2m)", IEEE 14th International Conference on Application-specific Systems, Architectures and Processors (ASAP), 24-26 de junio, 2003, pags. 444-454, consiste en usar un multiplicador completo para el paso de reducción C(x)-C1(x)*R(x). Sin embargo, una multiplicación completa adicional en este punto es muy negativa para la rapidez de la implementación de ECC.
Por el documento US2003/0208518 A1 (Figura 32 de dicho documento) se conoce la realización de un paso de cálculo C'(x)=C1(x)*(M-xm)+xn-m+C0(x) en la reducción multiplicativa de polinomios con orientación centrada, hasta que desaparece la parte sobresaliente del polinomio resultante. En este contexto, M designa un polinomio irreducible. El procedimiento incluye el paso consistente en almacenar el polinomio de reducción sin el término xm desplazado hacia la izquierda n-m posiciones y rellenar las posiciones marginales a la izquierda y la derecha con el valor cero. Para una implementación de 233 bits (m=233) con M=x233+x74+1 en un hardware de 256 bits (n=256), resulta (M-xm)*xn-m= (x74+1)* x256-233=x97+x23. Este polinomio reutilizable para todo el proceso de reducción se multiplica por la parte sobresaliente C1(x) y se añade a C0(x) (XOR), hasta que C1(x) es igual a cero. Por consiguiente, se requieren repetidas multiplicaciones completas de polinomios. A continuación, el polinomio reducido equivalente así calculado se desplaza hacia la izquierda mediante una multiplicación por xm.
En una variante descrita en el documento US2003/0208518 A1 (Figura 33) está previsto utilizar un polinomio parcialmente reducido en lugar del polinomio original para el cálculo de operaciones de multiplicación puntual, para a continuación llevar a cabo la reducción correspondientemente al procedimiento arriba descrito. De este modo, con una implementación se pueden realizar operaciones en los campos GF(2m) con valores m diferentes.
En el documento US2003/0182340 A1 se da a conocer un dispositivo de cálculo de valor residual a través de un campo de Galois, que funciona a un ritmo lento y que es especialmente adecuado para un cálculo de valor residual que puede ser utilizado en un procedimiento criptográfico en el que se emplean curvas elípticas. Para ello se propone una disposición de diferentes funciones lógicas y un esquema del funcionamiento de esta disposición. En este caso se multiplican dos expresiones... [Seguir leyendo]
Reivindicaciones:
1. Procedimiento utilizable en un procedimiento criptográfico en un dispositivo electrónico para reducir una primera palabra de datos binaria, que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1, a una segunda palabra de datos con una longitud máxima igual a m, que corresponde a un polinomio C''0(x) equivalente a C(x) en un campo finito binario GF(2m) cuyos elementos tienen una longitud máxima igual a m, siendo m menor o igual que n, que incluye los siguientes pasos:
- preparación de un polinomio de reducción R(x) consistente en un trinomio o un pentanomio;
- partición de la primera palabra de datos en una primera subpalabra de datos binaria C0 y una segunda subpalabra de datos binaria C1 cuyos polinomios correspondientes, C0(x) y C1(x), satisfacen la ecuación C(x)=C1(x)*xm+C0(x), y toma de la segunda subpalabra de datos para formar un primer término de sumandos;
- desplazamiento a la derecha de la segunda subpalabra de datos para formar un segundo término de sumandos, y repetición del paso de desplazamiento a la derecha para formar otros términos de sumandos hasta que cada término que no desaparezca del polinomio de reducción, que no sea el término xm, tenga asignado un término de sumandos, siendo la anchura de paso de cada desplazamiento a la derecha igual a la diferencia entre m y el orden de un término correspondiente que no desaparece del polinomio de reducción;
- adición de los términos de sumandos formados a la primera subpalabra de datos para formar una palabra de datos de suma;
- si la palabra de datos de suma así determinada tiene una longitud mayor que m, aplicación de los pasos de procedimiento a partir del paso de partición a la palabra de datos de sumandos formada, hasta que la palabra de datos de suma así determinada tenga una longitud máxima igual a m y por consiguiente constituya la segunda palabra de datos.
2. Procedimiento utilizable en un procedimiento criptográfico en un dispositivo electrónico para reducir una primera palabra de datos, que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1, a una segunda palabra de datos con una longitud máxima igual a m, que corresponde a un polinomio C''0(x) equivalente a C(x) en un campo finito binario GF(2m) cuyos elementos tienen una longitud máxima igual a m, siendo m menor o igual que n, que incluye los siguientes pasos:
- preparación de un polinomio de reducción R(x) consistente en un trinomio o un pentanomio;
- partición de la primera palabra de datos en una primera subpalabra de datos binaria C0 y una segunda subpalabra de datos binaria C1 cuyos polinomios correspondientes, C0(x) y C1(x), satisfacen la ecuación C(x)=C1(x)*xm+C0(x), y toma de la segunda subpalabra de datos para formar un primer término de sumandos;
- desplazamiento a la derecha de la segunda subpalabra de datos para formar un segundo término de sumandos, y repetición del paso de desplazamiento a la derecha para formar otros términos de sumandos hasta que cada término que no desaparezca del polinomio de reducción, que no sea el término xm, tenga asignado un término de sumandos, siendo la anchura de paso de cada desplazamiento a la derecha igual a la diferencia entre m y el orden de un término correspondiente que no desaparece del polinomio de reducción;
- adición de los términos de sumandos formados, a excepción del último término de sumandos asignado al término x0, a la primera subpalabra de datos;
- si la palabra de datos de suma así determinada tiene una longitud mayor que m, aplicación de los pasos de procedimiento a partir del paso de partición a la palabra de datos de sumandos formada, hasta que la palabra de datos de suma así determinada tenga una longitud máxima igual a m;
- adición del último término de sumandos y, en el caso mencionado de una aplicación de los pasos de procedimiento a partir del paso de partición a la palabra de datos de sumandos formada, de cada último término de sumandos determinado entre tanto, a la palabra de datos de suma determinada en último lugar para formar la segunda palabra de datos.
3. Procedimiento según la reivindicación 1 o 2, en el que la primera palabra de datos tiene una longitud menor que 2n-1, con un primer paso de justificación adicional realizado antes de la operación de desplazamiento a la derecha, que incluye un desplazamiento a la izquierda de la primera palabra de datos con una anchura de paso de relleno y una adición de una cantidad de ceros correspondiente a la anchura de paso de relleno a ambos lados de la primera palabra de datos, de tal modo que la longitud de la primera palabra de datos así modificada es igual a 2n-1 y que, en la primera palabra de datos modificada, aquellos términos del polinomio C(x) correspondiente a la primera palabra de datos que tienen un orden mayor que m están dispuestos en las mismas posiciones de bit que ocuparían si la primera palabra de datos ya hubiera tenido desde un principio la longitud 2n-1.
4. Procedimiento según la reivindicación 3, con un segundo paso de justificación que incluye una eliminación de los ceros añadidos inicialmente a la palabra de datos de suma determinada y un desplazamiento a la derecha de la palabra de datos de suma en una distancia correspondiente a la anchura de paso de relleno.
5. Procedimiento según una de las reivindicaciones 1 a 4, en el que el polinomio irreducible se representa exclusivamente mediante las potencias de los términos que no desaparecen del polinomio de reducción y que no son el término xm.
6. Procedimiento según la reivindicación 5, en el que el polinomio irreducible se representa adicionalmente mediante la longitud máxima conocida m de las palabras de datos del campo finito binario.
7. Procedimiento criptográfico asimétrico utilizable en un dispositivo criptográfico electrónico, que incluye
- la reducción de una primera palabra de datos, que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1, a una segunda palabra de datos con una longitud máxima igual a m, que corresponde a un polinomio C''0(x) equivalente a C(x) en un campo finito binario GF(2m) cuyos elementos tienen una longitud máxima igual a m, siendo m menor o igual que n, según una de las reivindicaciones 1-6.
8. Procedimiento criptográfico asimétrico según la reivindicación 7, que constituye un procedimiento de criptografía de curva elíptica, que antes de la reducción incluye
- la multiplicación de dos palabras de datos factor correspondientes a polinomios factor A(x) y B(x) para obtener la primera palabra de datos que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1.
9. Procedimiento para el cálculo de una firma digital, que incluye un procedimiento criptográfico asimétrico según la reivindicación 8.
10. Dispositivo para reducir una primera palabra de datos, que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1, a una segunda palabra de datos con una longitud máxima igual a m, que corresponde a un polinomio C''0(x) equivalente a C(x) en un campo finito binario GF(2m) cuyos elementos tienen una longitud máxima igual a m, siendo m menor o igual que n, que incluye:
- una memoria que contiene una representación de al menos un polinomio de reducción R(x) consistente en un trinomio o un pentanomio;
- una unidad de selección configurada para tomar una subpalabra de datos binaria de la primera palabra de datos, cuyo polinomio correspondiente C1(x) satisface la ecuación C(x)= C1(x)*xm+C0(x) y que constituye un primer término de sumandos;
- una unidad de desplazamiento que está conectada con la unidad de selección y configurada para desplazar la subpalabra de datos a la derecha con una anchura de paso predeterminada en cada caso con el fin formar un segundo término de sumandos o términos de sumandos adicionales, y para emitir los términos de sumandos formados;
- una unidad de adición que está conectada con la unidad de desplazamiento y configurada para añadir a la primera palabra de datos un término de sumandos correspondiente y también los sumandos emitidos por la unidad de desplazamiento; y
- una unidad de control configurada para
determinar la anchura de paso de un desplazamiento a la derecha correspondiente a realizar por la unidad de desplazamiento con el fin de formar un término de sumandos como la diferencia entre m y el orden de un término correspondiente que no desaparece del polinomio de reducción;
dar instrucciones a la unidad de desplazamiento para que repita la realización del paso de desplazamiento a la derecha con el fin de formar otros términos de sumandos con una anchura de paso determinada de nuevo en cada caso, hasta que cada término que no desaparezca de un polinomio de reducción predeterminado en cada caso, y que no sea el término xm, tenga asignado un término de sumandos;
dar instrucciones a la unidad de adición para que añada los términos de sumandos correspondientes a la primera palabra de datos, con el fin de determinar una palabra de datos de suma;
y, en caso necesario, activar de nuevo la unidad de cálculo, la unidad de desplazamiento y la unidad de adición, hasta que una palabra de datos de suma determinada presente una longitud máxima igual a m y, en consecuencia, constituya la segunda palabra de datos.
11. Dispositivo según la reivindicación 10, en el que la unidad de control está configurada para, en caso de una repetición de los pasos de procedimiento a partir del paso consistente en la determinación de una subpalabra de datos binaria, dar instrucciones a la unidad de adición para que sume los términos de sumandos formados en cada caso, a excepción del primer término de sumandos, a la primera palabra de datos correspondiente,
y para que, después de comprobar que una palabra de datos de suma determinada tiene una longitud no mayor que m, sume cada primer término de sumandos determinado entre tanto a la palabra de datos de suma determinada con el fin de formar la segunda palabra de datos.
12. Dispositivo según la reivindicación 10 u 11, con una primera y una segunda unidad de justificación,
estando configurada la primera unidad de justificación para desplazar a la izquierda una distancia correspondiente a una anchura de paso de relleno una primera palabra de datos entrante, que presenta una longitud menor que 2n-1, antes de la operación de desplazamiento a la derecha, y añadir a la primera palabra de datos, a ambos lados de la misma, una cantidad de ceros correspondiente a la anchura de paso de relleno, de tal modo que la longitud de la primera palabra de datos así modificada es igual a 2n-1 y que, en la primera palabra de datos modificada, aquellos términos del polinomio C(x) correspondiente a la primera palabra de datos que tienen un orden mayor que m están dispuestos en las mismas posiciones de bit que ocuparían si la primera palabra de datos ya hubiera tenido desde un principio la longitud 2n-1; y
estando configurada la segunda unidad de justificación para desplazar a la derecha una distancia correspondiente a la anchura de paso de relleno la palabra de datos de suma determinada con una longitud máxima igual a m, y retirar los ceros añadidos al principio.
13. Dispositivo según una de las reivindicaciones 10 a 12, en el que la unidad de desplazamiento incluye una serie de dispositivos de desplazamiento a la derecha conectados en paralelo, a los que se lleva la subpalabra de datos.
14. Dispositivo según una de las reivindicaciones 10 a 12, en el que la unidad de desplazamiento incluye exactamente un dispositivo de desplazamiento a la derecha y la unidad de control está configurada para llevar a cabo la repetición del paso de desplazamiento a la derecha para formar otros términos de sumandos mediante un desplazamiento adicional a la derecha del término de sumandos indicado en último lugar por el dispositivo de desplazamiento a la derecha con una anchura de paso de diferencia correspondiente, consistiendo la anchura de paso de diferencia correspondiente en la diferencia entre los desplazamientos a la derecha de términos de sumandos sucesivos en cada caso con respecto al primer término de sumandos.
15. Dispositivo criptográfico electrónico que incluye un dispositivo de reducción según una de las reivindicaciones 10 a 14.
16. Dispositivo criptográfico electrónico según la reivindicación 15, que está configurado para la codificación o descodificación de datos de acuerdo con un procedimiento de criptografía de curva elíptica.
17. Dispositivo criptográfico electrónico según la reivindicación 16, con un dispositivo multiplicador configurado para multiplicar dos palabras de datos factor correspondientes a polinomios factor A(x) y B(x) para obtener una primera palabra de datos que corresponde a un polinomio C(x) y que presenta una longitud máxima de 2n-1.
Patentes similares o relacionadas:
Sistema y método de exponenciación del teorema chino del resto de uso único para algoritmos criptográficos, del 6 de Noviembre de 2019, de Thales Dis France SA: Un método para operar un aparato de criptografía para realizar una operación de descifrado que tiene una operación de exponenciación X, protegiendo el método al […]
Multiplicador no modular, procedimiento para multiplicación no modular y dispositivo computacional, del 17 de Julio de 2019, de Winbond Electronics Corp: Un multiplicador no modular, que comprende: una interfaz , que está configurada para recibir números A y B enteros de n bits; y circuitería […]
Procedimiento de cálculo, dispositivo de cálculo y producto de software de cálculo para dominio de Montgomery, del 16 de Enero de 2019, de Winbond Electronics Corp: Un procedimiento de cálculo, que comprende: recibir, en un circuito multiplicador de Montgomery, un par de coordenadas (x, y) de […]
Método, dispositivo y medio legible por ordenador no transitorio para cálculo criptográfico, del 4 de Julio de 2018, de Winbond Electronics Corp: Un método para cálculo criptográfico, que comprende: recibir , en un circuito multiplicador de Montgomery que tiene un tamaño de bloque predeterminado, un par de […]
Procedimiento para codificar o decodificar con seguridad un mensaje, del 31 de Agosto de 2016, de SIEMENS AKTIENGESELLSCHAFT: Procedimiento para codificar o decodificar de forma segura un mensaje o para generar o verificar una firma digital de un mensaje, en el que con […]
Procedimiento de procesamiento criptográfico de datos y dispositivo asociado, del 18 de Septiembre de 2013, de OBERTHUR TECHNOLOGIES: Procedimiento de procesamiento criptográfico de datos aplicado dentro de una entidad electrónica, en el que sedetermina, a partir de un primer punto en una […]
Criptografía sobre una curva elíptica simplificada, del 7 de Agosto de 2013, de MORPHO: Un procedimiento de ejecución de un cálculo criptográfico en un componente electrónico que comprende unaetapa de obtención de un punto P(X,Y) a partir de al menos un […]
Uso de un coprocesador para inversión modular, del 27 de Mayo de 2013, de GIESECKE & DEVRIENT GMBH: Procedimiento para el uso de un coprocesador para la determinación del inverso modular x de un valor deentrada u con respecto a un módulo v, en el que: - […]