MÉTODO Y SISTEMA DIGITAL PROBABILÍSTICO PARA LA EXPLORACIÓN EFICIENTE DE GRANDES BASES DE DATOS.
Sistema digital probabilístico para la exploración eficiente de grandes bases de datos que comprende una entrada de n+1 vectores,
de los cuales `n' pertenecen a la base de datos y uno es el patrón a identificar vector x0 (1); donde cada vector consistirá en N números o descriptores definidos por `m' bits cada uno, y donde cada uno de estos componentes de `m' bits representarán un descriptor determinado para el objeto que describe cada vector; de tal forma que cada objeto viene determinado por N descriptores distintos codificados cada uno con `m' bits, y donde las cantidades que describe cada descriptor tendrán que ser normalizadas al rango que abarcan; y donde de la base de datos a escanear se volcarán un total de n vectores (2), cada uno de los cuales se comparará con el vector de referencia x0 (1)en una pluralidad de comparadores vectoriales (3).
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P201231295.
Solicitante: UNIVERSITAT DE LES ILLES BALEARS.
Nacionalidad solicitante: España.
Inventor/es: ROSELLÓ SANZ,José Luis, CANALS GUINAND,Vicente J, MORRO GOMILA,Antoni.
Fecha de Publicación: .
Clasificación Internacional de Patentes:
- G06F17/10 FISICA. › G06 CALCULO; CONTEO. › G06F PROCESAMIENTO ELECTRICO DE DATOS DIGITALES (sistemas de computadores basados en modelos de cálculo específicos G06N). › G06F 17/00 Equipo o métodos de procesamiento de datos o de cálculo digital, especialmente adaptados para funciones específicas (recuperación de la información, estructuras de las bases de datos o estructuras de los sistemas de archivos G06F 16/00). › Operaciones matemáticas complejas.
Fragmento de la descripción:
La presente invención se refiere al diseño de un circuito digital que es capaz de explorar de forma rápida y eficiente grandes bases de datos en la búsqueda de patrones concretos. La presente invención está adaptada para la computación masiva en paralelo y tiene una gran relevancia en muchas áreas de ciencia en donde se han de explorar grandes bases de datos para la extracción de información útil.
Antecedentes de la invención En [Gaines, B.R., 1968. “Random pulse machines”, IEEE Trans. on Comp. 410] se describe la idea de aplicar la teoría de probabilidades a los circuitos digitales con el fin de implementar operaciones algebraicas de forma sencilla y altamente inmune al ruido si la comparamos con la lógica digital tradicional. En este documento se utiliza el hecho que, partiendo de señales digitales pulsantes aperiódicas se pueden implementar operaciones aritméticas complejas como la suma o la multiplicación a partir de circuitos digitales sencillos (en estos dos casos dispondríamos de un multiplexor para la suma ponderada y de una puerta AND para la multiplicación) . Estas propiedades pueden ser usadas para la implementación de sistemas eficientes de reconocimiento de patrones.
La desventaja de esta forma de utilizar las puertas lógicas se presenta cuando se quiere almacenar o reconvertir la información de cada computación realizada en el sistema al mundo binario. Por cada canal estocástico de información que se desee conocer su actividad (y por tanto conocer el valor numérico que representa) se ha de integrar durante un tiempo suficiente el número de pulsos proporcionados por la señal. Este hecho hace que, en 25 caso de querer suficiente precisión en las mediciones, el tiempo de computación necesario para obtener determinadas operaciones será mucho mayor que el usado por la tecnología digital clásica que se utiliza actualmente. Este hecho hizo abandonar dicha tecnología a mediados de los setenta cuando surgieron los primeros microprocesadores basados en la lógica digital convencional y que proporcionaban altas precisiones en menores tiempos de computación. Otra de las características diferenciadoras de este tipo de lógica es la necesidad de la descorrelación entre las señales que se operan. Esta descorrelación temporal de las señales es necesaria para poder implementar las operaciones aritméticas básicas. Hay que reseñar que, en los principios de la computación, la lógica estocástica se postulaba como una lógica alternativa a la lógica digital tradicional y que por tanto su aplicación es tan generalista como ésta. La principal razón de su entrada en desuso y olvido (durante la década de los 70) se debió a la falta de precisión en las operaciones que se realizaban (debido a su naturaleza probabilística) y debido sobretodo a la necesidad de usar sistemas deterministas de gran precisión para automatizar las actividades económico-financieras tanto en el ámbito doméstico como empresarial, que se correspondía con el principal sector demandante de sistemas de computación.
De esta forma la computación estocástica o probabilística no se desarrollará durante los años siguientes aunque ésta haya sido utilizada últimamente para la implementación de redes neuronales en hardware [Y. Maeda and Y. Fukuda, “FPGA Implementation of Pulse Density Hopfield Neural Network”, In Proc. Int. Joint Conf. on Neural Networks, Florida, USA, 2007; Kondo Y, Sawada, Y, 1992. “Functional Abilities of a Stochastic Logic Neural Network” IEEE Trans. on Neural Networks, 3 (3) , 434-443; S. Sato, K. Nemoto, S. Akimoto, M Kinjo and K. Nakajima, “Implementation of a New Neurochip Using Stochastic Logic” IEEE Trans. on Neural Networks, 14 (5) , 45 Sept 2003, pp. 1122-1127; S. L. Bade, B. Hutchings. “FPGA-Based Stochastic Neural Networks Implementation” in Proc. IEEE Workshop on FPGAs for Custom Computing Machines, Napa Valley, CA, USA, 1994. pp. 189-198;
B. Brown, H. Card, “Stochastic Neural Computation I: Computational Elements” IEEE Transactions on Computers, Volume. 50, Issue. 9, pp. 891–905, 2001].
A medida que la tecnología de integración de los circuitos ha evolucionado desde finales de la década de 1950 hasta la actualidad se han incrementado exponencialmente el número de transistores que se pueden implementar en un solo integrado. Según la conocida ley de Moore, cada dos años la tecnología dobla sus prestaciones. Esto implica por ejemplo que en un período de 20 años (desde principios de los 90 hasta ahora) la tecnología se haya multiplicado por un factor 1000 o más, permitiendo actualmente la integración de miles de 55 millones de transistores en un solo integrado.
Este nuevo escenario abre grandes posibilidades para el uso de lógicas no-deterministas como la lógica estocástica o probabilística en aplicaciones en donde se necesite gran paralelismo y no sea necesario conocer oalmacenar los resultados parciales de la computación de cada módulo estocástico que esté operativo. Éste es el caso por ejemplo de los sistemas de reconocimiento de formas en donde a partir de una gran cantidad de información de entrada y de la realización probabilística de muchos procesos en paralelo se determine si determinado estímulo complejo pertenece o no a una categoría concreta. En el caso concreto de la exploración de grandes bases de datos el proceso consiste en identificar el conjunto de vectores de la base de datos que mejor coincidan con el patrón modelo que se esté buscando. De esta forma, y gracias al reducido tamaño de las 65 estructuras lógicas que requieren los elementos computacionales estocásticos o probabilísticos se pueden incrementar considerablemente el número de estos bloques a la vez que la velocidad de proceso de éstos,
posibilitando así la computación masiva en paralelo. Recientes trabajos [V Canals, A. Morro, J.L. Rosselló, “Stochastic-Based pattern-recognition analysis” Pattern Recognition Letters 20101101 Elsevier] realzan este hecho y demuestran por ejemplo que para el caso concreto del reconocimiento de patrones la lógica estocástica es ordenes de magnitud más rápida que la lógica tradicional basada en microprocesadores, lo cual puede ser
considerado, en este campo concreto, como una gran ventaja de esta tecnología con respecto a la tradicional.
Por tanto, el problema técnico que pretende resolver la presente invención es la identificación comparativa de objetos a partir de una población determinada de objetos definidos por vectores en la base de datos.
En el documento [“Hardware implementation of stochastic-based Neural Networks”, Rossello J L; Canals V; Morro A. Proceedings of the International Joint Conference on Neural Networks -2010 IEEE World Congress on Computational Intelligence, WCCI 2010 - 2010 International Joint Conference on Neural Networks, IJCNN 2010] se divulgan elementos hardware para implementar sistemas basados en redes neuronales a partir de señales pulsantes. Se utilizan señales binarias pulsantes descorrelacionadas para la realización de comparaciones rápida y eficiente.
En [“Practical hardware implementation of self-configuring neural networks”, Rossello J L; Canals V; Morro A; De Paul I. Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) - Advances in Neural Networks - ISNN 2009 - 6th International Symposium on Neural Networks, ISNN 2009, Proceedings – 2009] se presenta una revisión sobre elementos HW eficientes para implementar redes neuronales que permiten generar vectores aleatorios y donde se muestra un prototipo de bajo coste que combina una puerta lógica XOR y un element N-bit shift register.
En [“Using stochastic logic for efficient pattern recognition analysis”, Rossello J L; Canals V; De Paul I; Segura J.
Proceedings of the International Joint Conference on Neural Networks - 2008 International Joint Conference on Neural Networks, IJCNN 2008 – 2008] se divulga una metodología probabilística de reconocimiento de patrones basada en comparaciones en paralelo. Se presenta un sistema digital que permite obtener la señal más próxima al patrón utilizando puertas lógicas y bloques comparadores. Las señales pulsantes que se utilizan deben de estar descorrelacionadas entre ellas para poder realizar las operaciones.
El documento US2005108675 “Pattern recognition method for integrated circuit design, involves iteratively comparing rank in tree representation of design instance built around each design unit with related rank in pattern tree for each design unit in list” que se refiere a un sistema digital para un circuito integrado que permite el reconocimiento...
Reivindicaciones:
1. Sistema digital probabilístico para la exploración eficiente de grandes bases de datos del tipo que comprende una entrada de n+1 vectores, de los cuales ‘n’ pertenecen a la base de datos y uno es el patrón a identificar
vector X0 (1) ; donde cada vector consistirá en N números o descriptores definidos por ‘m’ bits cada uno por lo que cada vector constará de un total de m*N bits, y donde cada uno de estos componentes de ‘m’ bits representarán un descriptor determinado para el objeto que describe cada vector; de tal forma que cada objeto viene determinado por N descriptores distintos codificados cada uno con ‘m’ bits, y donde las cantidades que describe cada descriptor tendrán que ser normalizadas al rango que abarcan; y donde de la base de datos a escanear se volcarán un total de n vectores (2) , cada uno de los cuales se comparará con el vector de referencia X0 (1) en una pluralidad de comparadores vectoriales (3) ; todo ello caracterizado porque:
como resultado de dicha comparación se genera para cada vector Xk que se compare con X0, una señal sk de 1 bit (4) que presenta una actividad irregular estocástica con probabilidad de activación proporcional a la similitud entre los vectores comparados X0 y Xk; todo ello de tal forma que para cada vector de los ‘n’ vectores 15 seleccionados de la base de datos se obtienen ‘n’ bits pulsantes con probabilidad de activación proporcional a la similitud entre vectores, y donde dichos bits están conectados con un bloque de comparación global de pulsos (5) cuya salida (6) codifica cuál de los ‘n’ bits es mayor;
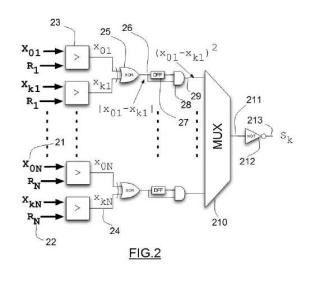
donde además, el comparador vectorial (3) comprende medios de comparación (21, 22, 23) para generar N señales pulsantes estocásticas correlacionadas entre sí y medios para la realización de operaciones aritméticas (27, 28, 29) con dichas señales descorrelacionadas;
donde además, cada comparador vectorial (3) comprende al menos un comparador binario (23) con dos entradas (21, 22) , en donde una primera entrada (21) está conectada con los descriptores que consisten en números binarios de ‘m’ bits X0j y Xkj donde j es un número entero entre 1 y N definiendo al descriptor j-ésimo y la segunda entrada (22) consiste en un número aleatorio de ‘m’ bits Rj; todo ello de tal forma que como resultado de dichas comparaciones se generarán ‘N’ señales pulsantes estocásticas (x0j, xkj) a la salida (24) de cada comparador (23) ; y donde estas señales de salida (24) están conectadas con un puerta XOR (25) cuya salida (26) es una señal pulsante estocástica cuya probabilidad de activación es proporcional a la distancia entre descriptores; y donde dicha señal estocástica se puede elevar al cuadrado si se la multiplica por ella misma mediante una puerta AND (28) , descorrelacionando las señales mediante un registro de desplazamiento (27) , obteniendo a la salida de la puerta AND (29) una señal pulsante estocástica con probabilidad de activación igual a (x0j – xkj) 2;
y donde además, para cada componente de los vectores que se comparan, se replica la estructura para obtener la señal de salida de la puerta AND (29) ; que están conectadas con la entrada de un multiplexor (210) que se encarga de pasar a su salida (211) todas y cada una de sus N entradas de forma secuencial, cuyo resultado es una señal pulsante (211) con probabilidad de activación igual al valor medio de las señales de activación Σj (x0j–xkj) 2/N, siendo esta probabilidad proporcional al cuadrado de la distancia euclidiana entre los vectores que se comparan.
2. Sistema de acuerdo con la reivindicación 1 donde el bloque de comparación global de pulsos (5) tiene un tiempo de respuesta determinado T que estará en función de los contadores internos del comparador global de pulsos (5) .
3. Sistema de acuerdo con la reivindicación 1 donde la señal pulsante (211) de salida del multiplexor (210) se invierte la señal con un inversor (212) de forma que se obtiene una señal con probabilidad de activación Sk=1
Σj (x0j–xkj) 2/N (4) ; donde este parámetro será 1 cuando ambos vectores sean iguales mientras que tiende a cero a medida que las distancias entre vectores aumenta.
4. Sistema de acuerdo con la reivindicación 1 donde los números aleatorios Rj serán generados por distintos bloques que tanto podrán ser generadores de números pseudo-aleatorios como las LFSR (31) como generadores de números aleatorios basados en sistemas caóticos ó estocásticos.
5. Sistema de acuerdo con la reivindicación 4 en donde los LFSR (31) son inicializados por una señal de inicio global (32) y que proporcionarán a su salida (33) un número aleatorio de ‘m’ bits cada flanco de la señal de reloj (34) .
5.
6. Sistema de acuerdo con cualquiera de las reivindicaciones anteriores en donde el comparador global de pulsos (5) para cada entrada de similitud Si (i=1..n) de cada comparación realizada se conecta a un contador, de tal forma que las ‘n’ entradas (41) se conectan a dichos contadores (42) que en caso de desbordar su cuenta activan su salida (43) yi, que a su vez activa el reset síncrono (45) mediante una puerta OR (44) de todos los contadores que no han llegado a desbordar; y donde su vez, la señal yi (43) es capturada por un elemento de memoria (flip-flop D) (46) que proporciona a su salida la codificación de cuál es el vector más parecido a la referencia x0; y donde la salida (47) de cada Flip-Flop (46) se actualiza en el momento que la señal de habilitación (48) se activa y que coincide con la señal de reset síncrono (45) , obteniendo a la salida (6) del comparador global de pulsos (5) un bus de ‘n’ bits con todos los bits puestos a 0 excepto el bit correspondiente al
vector más próximo al de referencia.
7. Método para la exploración eficiente de grandes bases de datos implementado en un sistema según cualquiera de las reivindicaciones anteriores que comprende una entrada de n+1 vectores, de los cuales ‘n’ pertenecen a la base de datos y uno es el patrón a identificar vector X0 (1) ; donde cada vector consistirá en N números o descriptores definidos por ‘m’ bits cada uno por lo que cada vector constará de un total de m*N bits, y
donde cada uno de estos componentes de ‘m’ bits representarán un descriptor determinado para el objeto que describe cada vector; de tal forma que cada objeto viene determinado por N descriptores distintos codificados cada uno con ‘m’ bits, y donde las cantidades que describe cada descriptor están normalizadas al rango que abarcan; caracterizado porque comprende:
un volcado de la base de datos a escanear de un total de n vectores (2) , cada uno de los cuales se compara con el vector de referencia X0 (1) en una pluralidad de comparadores vectoriales (3) ; y donde como resultado de dicha comparación se genera para cada vector Xk que se compare con X0, una señal sk de 1 bit (4) que presenta una actividad irregular estocástica con probabilidad de activación proporcional a la similitud entre los vectores comparados X0 y Xk; todo ello de tal forma que para cada vector de los ‘n’ vectores seleccionados de la base de datos se obtienen ‘n’ bits o señales pulsantes con probabilidad de activación proporcional a la similitud entre vectores; y donde finalmente se establece una etapa de codificación de los ‘n’ bits definiendo cuál es el mayor; donde el comparador vectorial (3) comprende medios de comparación (21, 22, 23) para generar N señales pulsantes estocásticas correlacionadas entre sí y medios para la realización de operaciones aritméticas (27, 28, 29) con dichas señales descorrelacionadas;
donde cada comparador vectorial (3) comprende al menos un comparador binario (23) con dos entradas (21, 22) , en donde una primera entrada (21) está conectada con los descriptores que consisten en números binarios de ‘m’ bits X0j y Xkj donde j es un número entero entre 1 y N definiendo al descriptor j-ésimo y la segunda entrada (22) consiste en un número aleatorio de ‘m’ bits Rj; todo ello de tal forma que como resultado de dichas comparaciones se generarán ‘N’ señales pulsantes estocásticas (x0j, xkj) a la salida (24) de cada comparador
(23) ; y donde estas señales de salida (24) están conectadas con un puerta XOR (25) cuya salida (26) es una señal pulsante estocástica cuya probabilidad de activación es proporcional a la distancia entre descriptores; y donde dicha señal estocástica se puede elevar al cuadrado si se la multiplica por ella misma mediante una puerta AND (28) , descorrelacionando las señales mediante un registro de desplazamiento (27) , obteniendo a la salida de la puerta AND (29) una señal pulsante estocástica con probabilidad de activación igual a (x0j – xkj) 2;
y donde, para cada componente de los vectores que se comparan, se replica la estructura para obtener la señal de salida de la puerta AND (29) ; que están conectadas con la entrada de un multiplexor (210) que se encarga de pasar a su salida (211) todas y cada una de sus N entradas de forma secuencial, cuyo resultado es una señal pulsante (211) con probabilidad de activación igual al valor medio de las señales de activación Σj (x0j– xkj) 2/N, siendo esta probabilidad proporcional al cuadrado de la distancia euclidiana entre los vectores que se comparan.
8. Uso del sistema según cualquiera de las reivindicaciones 1 a 6 en la identificación de moléculas candidatas a posibles fármacos a partir de grandes bases de datos moleculares.
Patentes similares o relacionadas:
DISPOSITIVO ELECTRÓNICO CALCULADOR DE FUNCIONES TRIGONOMÉTRICAS, del 25 de Mayo de 2020, de UNIVERSIDAD DE SEVILLA: En este documento se detalla un dispositivo electrónico que permite calcular una serie de funciones matemáticas, más concretamente una serie de funciones trigonométricas […]
DISPOSITIVO ELECTRÓNICO CALCULADOR DE FUNCIONES TRIGONOMÉTRICAS Y USOS DEL MISMO, del 25 de Mayo de 2020, de UNIVERSIDAD DE SEVILLA: Dispositivo electrónico calculador de funciones trigonométricas y usos del mismo. En este documento se detalla un dispositivo electrónico que permite calcular una serie […]
Procedimiento para predecir el flujo de fluido, del 1 de Abril de 2020, de EXXONMOBIL UPSTREAM RESEARCH COMPANY: Un procedimiento implementado por ordenador para mejorar un modelo geológico de una región bajo la superficie, que comprende: (a) obtener la […]
Método de notificación de congestión, sistema y dispositivo relacionados, del 26 de Junio de 2019, de HUAWEI TECHNOLOGIES CO., LTD.: Un método de notificación de congestión, caracterizado por cuanto que el método comprende: la recepción, por una entidad de función de exposición de capacidad […]
Cuantificador vectorial, del 19 de Junio de 2019, de TELEFONAKTIEBOLAGET LM ERICSSON (PUBL): Método para codificación de región de pico realizada por un códec de transformación que comprende un Cuantificador Vectorial, comprendiendo […]
Desarrollo y utilización de sondas fluorescentes de bilirubina no enlazada, del 1 de Mayo de 2019, de Kleinfeld, Alan M: Una composición que comprende: (a) una sonda que se une a la bilirrubina pero que no se une significativamente al ácido graso, comprendiendo dicha sonda una […]
 Métodos de análisis de campos electromagnéticos para materiales conductores anisotrópicos, del 26 de Abril de 2019, de Subaru Corporation: Un método de análisis del campo electromagnético para un material conductor anisotrópico, en el que el método de análisis del campo electromagnético utiliza […]
Métodos de análisis de campos electromagnéticos para materiales conductores anisotrópicos, del 26 de Abril de 2019, de Subaru Corporation: Un método de análisis del campo electromagnético para un material conductor anisotrópico, en el que el método de análisis del campo electromagnético utiliza […]
Aparato de codificación para el procesamiento de una señal de entrada y aparato de decodificación para el procesamiento de una señal codificada, del 31 de Enero de 2019, de FRAUNHOFER-GESELLSCHAFT ZUR FORDERUNG DER ANGEWANDTEN FORSCHUNG E.V.: Aparato de codificación para el procesamiento de una señal de entrada y aparato de decodificación para el procesamiento de una señal codificada. La […]