MÉTODO PARA REALIZAR UNA FIRMA DIGITAL DE GRUPO.

Método para realizar una firma digital de grupo.

Comprende:

i) generar, por una tercera parte de confianza (T), una clave privada para cada miembro (F1, F2, ..., Ft) de un grupo (G);

ii) seleccionar aleatoriamente, dicha tercera parte de confianza (T), un miembro de dicho grupo (G) para que actúe como firmante encargado de firmar un documento digital (M) en nombre del grupo (G);

iii) elaborar, dicho firmante, una firma digital de grupo usando su clave privada para firmar dicho documento digital (M); y

iv) verificar dicha firma digital de grupo.

El método comprende generar, por dicha tercera parte de confianza (T), una clave pública común para todos los miembros de dicho grupo (F{sub,1, F2, ..., Ft) y usar dicha clave pública común para realizar dicha verificación de la firma digital de grupo de la etapa iv).

Método para realizar una firma digital de grupo Campo de la técnica La presente invención se refiere, en general, a un método para realizar una firma digital de grupo, en la que un miembro seleccionado de un grupo firma un documento digital en nombre del resto de miembros del grupo, y más particularmente a un método que comprende usar una clave pública común para verificar la firma digital de grupo.

Estado de la técnica anterior

En la actualidad hay diferentes métodos y algoritmos para realizar, de manera segura, firmas electrónicas o digitales por medio de redes informáticas. La mayor parte de estos protocolos se basan en criptografía de clave pública (PKC) , (véase [ElG85], [MOV97], [RSA78]) . La característica principal de este tipo de criptografía es que cada individuo tiene dos claves, una clave pública, denominada e, y una clave privada, denominada d. La clave pública permite a cualquier usuario cifrar los mensajes dirigidos al propietario de la clave, usando un procedimiento de cifrado, E. Por tanto, esta clave se conoce públicamente. Por otro lado, la clave privada solo la conoce su propietario y es la que permite descifrar los mensajes cifrados recibidos, a través de un procedimiento de descifrado, D. Los procesos de cifrado y descifrado se indicarán, respectivamente, como Ek y Dk cuando se usa la clave k.

Los algoritmos, E y D, para cifrado y descifrado en protocolos de firma digital deben cumplir las siguientes condiciones:

1. El cifrado de un mensaje M con la clave pública, Ee, seguido de su descifrado con la clave privada, Dd, debe dar como resultado el mensaje original, es decir,

Dd (Ee (M) ) = Dd (c) = M.

2. El cifrado de un mensaje M realizado con una clave privada Ed, seguido por su descifrado realizado con la correspondiente clave pública De debe tener como resultado el mensaje original, es decir, los procedimientos E y D deben verificar que:

De (Ed (M) ) = De (c’) = M.

Además, para que los procedimientos de firmas digitales y su transmisión electrónica sean más eficaces, se usan funciones hash (véase [MOV97], [NIST02]) . Estas funciones calculan un hash o resumen del documento, de modo que es este resumen lo que se firma en última instancia, en lugar del documento completo. Las funciones hash se indicarán como H (·) a lo largo del presente documento.

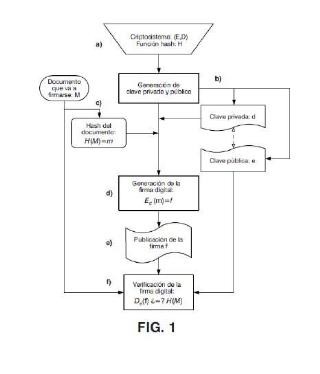
El procedimiento general para realizar la firma digital de un documento, M, sigue las siguientes etapas, tal como se muestra en la figura 1:

1. Seleccionar el criptosistema de clave pública, (E, D) , y la función hash, H, que van a usarse en el procedimiento de firma. El triplete (E, D, H) se conocerá públicamente.

2. Generar las claves pública y privada, e, d, del usuario que va a firmar el documento. Las claves también pueden proporcionarse por una tercera parte.

3. Calcular el resumen del mensaje que va a firmarse: H (M) = m.

4. Firmar digitalmente el resumen del mensaje usando la clave privada del firmante, d: Ed (m) = f.

5. Publicar el documento original y su correspondiente firma digital: (M, f) . A su vez, el verificador de la firma digital:

1. comprueba la corrección de la firma del documento firmado usando el mensaje publicado, M, la firma digital, f, y la clave pública del firmante, e, de la siguiente manera: De (f) = De (Ed (m) ) = m,

H (M) = m’, m’ =? m.

El desarrollo y la simplicidad con respecto al uso de ordenadores y el acceso generalizado a Internet para los ciudadanos han conducido a la aparición de nuevos métodos de firma digital. Hoy en día es posible abordar problemas que no tenían solución en el pasado.

Uno de estos problemas es cómo permitir que un único usuario firme digitalmente un documento de tal manera que la firma se realice en nombre de un grupo previamente determinado de usuarios (al que pertenece el firmante) . Este tipo de firma se conoce como firma de grupo o firma en nombre de un grupo.

Una firma de grupo es un protocolo de firma digital mediante el cual un miembro de un grupo de t firmantes,

G = {F1, F2, …, Ft},

firma un documento en nombre del resto de miembros del grupo (véase, por ejemplo, [ACJ00], [AM03], [BSZ05], [BBX04], [CL04], [CH91], [CHY05], [FC04], [NS04], [TW05]) .

Estos esquemas de firma muestran algunas características notables:

1. Sólo un miembro del grupo puede firmar de manera válida un documento o mensaje.

2. El receptor del mensaje firmado puede verificar que la firma es una firma de grupo válida, es decir, que se ha llevado a cabo por un miembro legítimo del grupo. Sin embargo, el receptor no podrá determinar qué miembro particular del grupo realmente firmó el mensaje.

3. Si se requiere (en caso de una disputa, por ejemplo) , es posible dar a conocer al firmante, es decir, revelar qué usuario firmó realmente el mensaje.

Las firmas de grupo pueden considerarse una generalización de esquemas de autenticación mediante credenciales, mediante las que una persona demuestra que pertenece a un grupo particular. En particular, pueden considerarse como una extensión de los mecanismos de credenciales propuestos por Chaum ([Cha85]) , y esquemas de autenticación de miembros ([OOK90], [SKI90]) , en los que un miembro de un grupo puede convencer a un verificador de que pertenece a un determinado grupo sin revelar su identidad.

Existen varias propuestas para firmas de grupo, que usan una serie de primitivas criptográficas (por ejemplo, [CH91]) . Algunas de estas propuestas necesitan una tercera parte de confianza (TTP) , al menos para el proceso de inicialización. Otros esquemas, sin embargo, permiten a cualquier usuario crear el grupo al que elige pertenecer.

Por regla general, las firmas de grupo hacen uso de esquemas cuya seguridad se basa en problemas matemáticos computacionalmente irresolubles. Normalmente, tales problemas son el problema de factorización de enteros (IFP) y el problema de logaritmo discreto (DLP) .

Tal como se muestra en la figura 2, el proceso más sencillo para llevar a cabo una firma digital de grupo es el siguiente:

1. La tercera parte de confianza, T, selecciona el criptosistema de clave pública, (E, D) , y la función hash, H, que van a usarse en el proceso de firma digital de grupo. T da a conocer el triplete (E, D, H) de manera pública.

2. T genera un par de claves pública y privada (ei, di) , i = 1, …, t, para cada uno de los usuarios en el grupo G.

3. T ordena aleatoriamente la lista de claves públicas de los usuarios y publica la lista ordenada.

4. Uno de los usuarios en G se selecciona aleatoriamente (la elección puede realizarla T) , sea F. Este firmante, cuyo par de claves se indica como (e, d) , llevará a cabo el proceso de firma en nombre del grupo.

5. F determina el hash del mensaje que va a firmarse: H (M) = m.

6. F realiza la firma digital del hash del mensaje usando su propia clave privada, d: Ed (m) = f.

7. T publica tanto el mensaje firmado como la firma de grupo calculada por F: (M, f) . El verificador de la firma digital:

1. Obtiene la lista de claves públicas de los usuarios en G.

2. Comprueba si la siguiente fórmula aplicada al mensaje publicado, M, se cumple cuando se usa una

de las claves públicas en la lista, e:

De (f) = De (Ed (m) ) = m,

H (M) = m’,

m’ =? m.

Si se cumple la fórmula para una de las claves públicas, el verificador está seguro de que la firma es válida, puesto que cada clave pública está asociada con una correspondiente clave privada. Sin embargo, el verificador no puede determinar quién fue el firmante real, ya que la lista de claves públicas se ha ordenado aleatoriamente.

Si el número de posibles firmantes es elevado, también lo es el número de claves públicas. Esto significa que el proceso de verificación puede conllevar una gran carga computacional ya que, en el peor de los casos, deben comprobarse todas las claves públicas antes de completarse la verificación.

Además de los esquemas ya mencionados, existen varias patentes relativas a firmas de grupo: [HCW06], [KT08], [MFM09], [MCGT10] y [Ter08].

Problemas con las soluciones existentes:

Los protocolos mencionados anteriormente muestran ciertas limitaciones.

Por ejemplo, los esquemas descritos en [ACJ00], [AM03], y [NS04] tienen un problema de seguridad (véase [SG02] para una explicación ampliada) . Además, la seguridad de los esquemas presentados en [BBX04] y [CL04] se prueba en condiciones artificiales y poco probables (véase [BB04]) .

Varias patentes muestran también algunos inconvenientes. Entre éstos se encuentra la...

1. Método para realizar una firma digital de grupo, que comprende:

i) generar, por una tercera parte de confianza (T) , una clave privada para cada miembro (F1, F2, …, Ft) de un grupo (G) ;

ii) seleccionar aleatoriamente, dicha tercera parte de confianza (T) , un miembro de dicho grupo (G) para que actúe como firmante encargado de firmar un documento digital (M) en nombre del grupo (G) ;

iii) elaborar, dicho firmante, una firma digital de grupo usando su clave privada para firmar dicho documento digital (M) ; y

iv) verificar dicha firma digital de grupo;

estando el método caracterizado porque comprende generar, por dicha tercera parte de confianza (T) , una clave pública común para todos los miembros de dicho grupo (F1, F2, …, Ft) y usar dicha clave pública común para realizar dicha verificación de la firma digital de grupo de la etapa iv) .

2. Método según la reivindicación 1, en el que dicha etapa iii) comprende elaborar, dicho firmante, dicha firma digital de grupo en un resumen (m) de dicho documento (M) .

3. Método según la reivindicación 2, en el que dicha elaboración de la firma digital de grupo de la etapa iii) se calcula como: fi = ai + ci · m (mod r) , gi = bi + di · m (mod r) donde i = 1, …, t; ai= (h – s · bi) (mod r) ; ci = (k – s · di) (mod r) ; bi, di son pares de números aleatorios generados por dicha tercera parte de confianza (T) ; m es el resumen o hash del documento (M) que va a firmarse; r es un número primo; s es un número secreto aleatorio generado por dicha tercera parte de confianza (T) ; h = (a0 + s · b0) (mod r) ;

h= (c0 + s · d0) (mod r) ; y a0, b0, c0, d0 son números enteros generados aleatoriamente por la tercera parte de confianza (T) .

4. Método según la reivindicación 3, en el que ai, ci, bi, di E Zr donde Zr es el conjunto de enteros módulo r, s > r y pertenece a un subgrupo Sr de Zn; donde Zn es el conjunto de enteros módulo n y a0, b0, c0, d0 E Zr son las clave privadas de la tercera parte de confianza (T) .

5. Método según la reivindicación 4, que comprende verificar, en iv) , la firma digital de grupo comprobando si se cumple la siguiente igualdad:

P · Qm = af · ºg (mod n)

donde P y Q forman dicha clave pública común, f y g son la firma digital de grupo, a E Z*n es un número entero elegido por la tercera parte de confianza (T) con orden multiplicativo r, módulo n, yº = as (mod n) .

6. Método según la reivindicación 5, en el que:

P = aai- bi (mod n) ;

Q = aci-di (mod n) ; 2v1.v2.p1.q1 (mod n) ;

a = g º = as (mod n) ;

n = p · q;

g es un elemento elegido aleatoriamente que cumple que g E Z*n cuyo orden es A (n) ;

p1, q1 son números primos;

u1 y u2 son números enteros, donde u1 = 2 · v1 y u2 = 2 · v2;

v1, v2 son primos entre sí;

p = u1 · r · p1 + 1;

q = u2 · r · q1 + 1;

< (n) = (p–1) (q–1) = u1 · u2 · r2 · p1 · q1; donde < (n) es la función phi de Euler; A (n) = mcm (p–1, q–1) = 2 · v1 · v2 · r · p1 · q1; donde mcm representa el mínimo común múltiplo, y A (n) es10 la función de Carmichael; y a cumple la condición: mcd (a, < (n) ) = mcd (a, u1 · u2 · r2 · p1 · q1) = 1 donde mcd es el máximo común divisor.