Método para el modelado del nivel de glucemia mediante programación genética.
Método para el modelado del nivel de glucemia mediante programación genética.
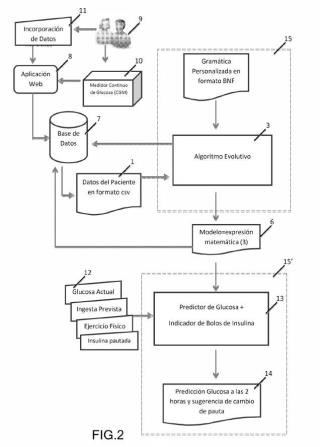
La invención consiste en un método que, aplicando algoritmos evolutivos sobre soluciones aleatorias y datos tomados de un paciente con glucemia, permite establecer un modelado del nivel de glucemia para obtener un modelado del nivel de glucosa en instantes futuros a los momentos de obtención de los datos del paciente. Los datos del paciente son al menos los niveles de glucosa, ingesta e insulina rápida y lenta para un intervalo de tiempo. El algoritmo evolutivo consiste básicamente en aplicar programación genética en su variante de gramáticas evolutivas o evolución gramatical. Es decir, aplicar gramáticas personalizadas en formato BNF, procesos de mapeo personalizados y evaluaciones de error concretas a las soluciones aleatorias o a modelos generados con anterioridad para obtener una expresión que describa y prediga los niveles de glucosa de un paciente. De entre todos los pacientes, el método de la presente invención está especialmente indicado para sujetos con Diabetes Mellitus.
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P201331726.
Solicitante: UNIVERSIDAD COMPLUTENSE DE MADRID.
Nacionalidad solicitante: España.
Inventor/es: HIDALGO PÉREZ,José Ignacio, GARNICA ALCAZAR,Antonio Oscar, LANCHARES DÁVILA,Juan, RISCO MARTÍN,Jose Luis, COLMENAR VERDUGO,Jose Manuel, CUESTA INFANTE,Alfredo, BOTELLA SERRANO,Marta, RUBIO GARCÍA,José Antonio, MAQUEDA VILLAIZÁN,Esther.
Fecha de Publicación: .
Clasificación Internacional de Patentes:
- G06F19/00
Fragmento de la descripción:
MÉTODO PARA EL MODELADO DEL NIVEL DE GLUCEMIA MEDIANTE PROGRAMACIÓN GENÉTICA
OBJETO DE LA INVENCIÓN
La presente invención propone aplicar la programación genética para encontrar un modelo personalizado que describa y prediga los niveles de glucosa de un paciente. De esta forma, la presente invención describe un método que, a partir de los datos históricos de un paciente que consisten en valores previos de glucosa, carbohidratos tomados e insulinas inyectadas, obtiene una expresión que puede usarse para predecir valores de glucosa en un futuro próximo.
El campo de aplicación de la presente invención es la estimación de la glucosa de un paciente a partir de los datos medidos. Debido a la naturaleza de la invención, la estimación de la glucosa de la presente invención permite a dispositivos que operen según el método de la presente invención, predecir los niveles de glucosa de un paciente. De entre todos los pacientes, el método de la presente invención está especialmente indicado para sujetos con Diabetes Mellitus.
ANTECEDENTES DE LA INVENCIÓN
La Diabetes Mellitus es una enfermedad causada por un defecto en la secreción o en la acción de la insulina, que es esencial para el control de los niveles de glucosa en sangre.
En ambos casos el resultado es que las células no asimilan el azúcar y como consecuencia, se produce una subida en los niveles de glucosa en sangre o hiperglucemia. Existen distintos tipos de diabetes dependiendo de su naturaleza. Según la ADA (American Diabetes Association) podemos distinguir cuatro tipos de DM:
Diabetes Tipo 1 (T1DM): Las células no producen insulina debido a un proceso autoinmune. Actualmente esto hace necesario que la persona se inyecte insulina exógena, ya sea mediante inyecciones puntuales o que utilice una bomba de insulina.
Diabetes Tipo 2 (T2DM): El es resultado de una resistencia a la insulina, donde las células no consiguen utilizar la insulina correctamente. En ocasiones se combina con una ausencia, ya sea parcial o total de insulina.
Diabetes Gestacional: Aparece en los periodos de gestación en una de cada diez mujeres embarazada. El embarazo es un cambio en el metabolismo, ya que el feto utiliza la energía de la madre para obtener alimento, oxigeno y otros recursos. Esto hace que se produzca un descenso en la secreción de insulina por parte de la madre.
Otros tipos: como por ejemplo problemas en las células , defectos genéticos que afectan a la acción de la insulina, provocados por medicamentos, síndromes genéticos, etc..
En la mayoría de los casos, los pacientes con una evolución larga de la enfermedad requieren la inyección de insulina exógena en varias dosis, o mediante una bomba de insulina. Es importante mantener un buen control glucémico para prevenir tanto las complicaciones agudas de la diabetes (cetoacidosis diabética e hipoglucemia, definida como un valor de glucosa en sangre inferior a 70mg=dl), como todas las complicaciones multi-crónicas asociadas a los pacientes diabéticos (nefropatía, retino patía, microangiopatía y macroangiopatía).
En los últimos años se ha demostrado que un control estricto del Nivel de glucemia en pacientes críticos mejora su evolución y reduce los costes médicos. El control de los niveles de glucosa es una tarea difícil y que requiere un esfuerzo por ambas partes, pacientes y sus familias. Para mantener buenos niveles de glucosa en sangre el paciente debe tener alguna capacidad de predicción para saber que nivel de glucosa tendría si toma cierta cantidad de comida o si se inyecta cierta cantidad de insulina de un determinado tipo. De hecho el objetivo final es evitar no sólo periodos de hiperglucemia (niveles de glucosa > 180 mg=dl) sino también episodios de Hipoglucemia severa (niveles de glucosa < 40mg=dl) que pueden llevar al paciente a la muerte.
Uno de los aspectos que hace difícil el control de glucosa en sangre es la ausencia de un modelo general de respuesta tanto a la insulina como a los diversos factores
mencionados anteriormente, debido principalmente a las particularidades de cada paciente.
Los modelos presentes en el estado de la técnica aplican técnicas de modelado clásico que resultan en el uso de ecuaciones lineales, perfiles definidos o modelos con un conjunto limitado de entradas.
Otro tipo de técnicas conocidas del estado de la técnica y que nunca han sido utilizadas para realizar modelos de estimación de la glucosa son las técnicas evolutivas. Las técnicas evolutivas como la programación genética (PG) tienen ciertas características que las hacen especialmente útiles para abordar problemas de optimización y modelado complejo. En primer lugar son "simples" conceptual mente hablando y también lo es su aplicación. Sin embargo tienen una base teórica bien definida y ampliamente estudiada. La programación genética ha demostrado su aplicabilidad a multitud de problemas reales y es intrínsecamente paralelizables por trabajar con un conjunto de soluciones. Es más, los algoritmos evolutivos tienen un gran potencial para incorporar conocimiento acerca del dominio en el que trabajan y para incorporar otros mecanismos de búsqueda no necesariamente evolutivos.
Una de las aplicaciones más conocidas de la programación genética es la regresión simbólica y la aplicación de una de las variantes de la PG, las gramáticas evolutivas o en inglés Grammatical Evolution (GE) nos permite obtener soluciones para incorporar términos no-lineales. La gramática evolutiva GE es una técnica de computación evolutiva establecida en 1998 por el grupo de Conor Ryan en la Universidad de Limerick (Irlanda). La programación genética trata de encontrar programas ejecutables o funciones que respondan a unos datos de referencia. La principal ventaja es que la gramática evolutiva GE aplica operadores genéticos a una cadena completa lo que simplifica la aplicación de la búsqueda en diferentes lenguajes de programación. Además no tiene problemas de memoria, al contrario que la programación genética básica, donde la representación en árbol puede llevar al conocido problema de bloating (un crecimiento excesivo de las estructuras de datos del computador en la memoria).
Por todo ello, nosotros proponemos aplicar PG para encontrar un modelo personalizado que describa y prediga los niveles de glucosa de un paciente. Nuestro método tomará los datos históricos de un paciente que consisten en valores previos de glucosa carbohidratos tomados e insulinas inyectadas y a partir de ellos obtendrá una expresión que puede usarse para predecir valores de glucosa en un futuro próximo.
Mediante los modelos del estado de la técnica no es posible conocer una estimación de la glucosa en sangre en pacientes ni de forma genérica ni personalizada al paciente. Ello implica que actualmente no es posible aplicar tratamientos adecuados a los pacientes con diabetes. Aunque existen muchos trabajos que usan modelos de control, hasta la fecha el problema del modelado no se ha abordado con técnicas de computación evolutiva. Esta solución no se ha abordado hasta la fecha debido a su complejidad mediante el uso de técnicas clásicas.
DESCRIPCIÓN DE LA INVENCIÓN
La presente invención propone una técnica nueva que implica obtener el modelo del paciente particularizado utilizando programación genética "GP" (del inglés "Genetic Programming"). La programación genética "GP" elimina las barreras relacionadas con la construcción del modelo, tales como la linealidad o la limitación en los parámetros de entrada. Mediante la aplicación de la programación genética "GP" en la forma divulgada por la presente invención, es posible encontrar un modelo personalizado que describa y prediga los niveles de glucosa de un paciente. El método de la presente invención toma los datos históricos de un paciente que consisten en valores previos de glucosa carbohidratos tomados e insulinas inyectadas y, a partir de ellos, obtiene una expresión que puede usarse para predecir valores de glucosa en un futuro próximo.
Un primer aspecto de la invención es un método para el modelado del nivel de glucemia que permite predecir la glucosa de un individuo. El método comprende los siguientes pasos:
i) obtener de un individuo unos datos que comprendan, para un tiempo k, al menos:
o unos niveles de glucosa GL\ o unos niveles de ingesta CH;
o unos niveles de insulina inyectada de efecto rápido IS e insulina inyectada de efecto lento /L;
ii) aplicar un Algoritmo Evolutivo a un conjunto de soluciones y a los datos anteriormente obtenidos;
iii) calcular una función GL de predicción de la glucosa para un tiempo posterior (k+1) al tiempo k, tal que:
GL(/e + 1) = /(GL, CH, IS, 1L).
...
Reivindicaciones:
1.- Método para el modelado del nivel de glucemia mediante programación genética que comprende los siguientes pasos:
i) obtener de un individuo unos datos que comprendan, para un tiempo k, al menos:
o unos niveles de glucosa GL\ o unos niveles de ingesta CH;
o unos niveles de insulina inyectada de efecto rápido IS e insulina inyectada de efecto lento /L;
ii) aplicar un Algoritmo Evolutivo a un conjunto de soluciones y a los datos anteriormente obtenidos;
iii) calcular una función GÍ de predicción de la glucosa para un tiempo posterior (k+1) al tiempo k, tal que:
Gl(k + 1) = f(GL, CH, IS, ¡L)
2 - Método según la reivindicación 1, caracterizado por que el paso ii) adicionalmente comprende llevar a cabo los siguientes pasos:
a) generar el conjunto de soluciones con N-soluciones aleatorias donde cada solución está formada por una cadena de caracteres (cromosoma);
b) calcular N-expresiones GLk para k=1,...,N obtenidas mediante la decodificación del conjunto de las N-soluciones aleatorias aplicando una gramática BNF y una función de mapeo;
c) calcular el error Ek que conlleva: calcular ek como la diferencia entre los datos obtenidos del paciente y las N-expresiones GLk; y, aplicar una función de fitness a cada uno de los errores anteriormente calculados ek; de tal forma que se obtiene para cada expresión GLk, un error asociado Ek;
d) seleccionar N-1 soluciones resultado de: tomar las N-soluciones y apartar la solución de menor error Ek de las N-soluciones; enfrentar las N-1 soluciones tomadas de dos en dos, seleccionando la solución de menor error Ek;
e) cruzar las N-1 soluciones anteriores mediante un algoritmo de probabilidad de cruce;
f) mutar un carácter de las N-1 soluciones anteriores mediante un algoritmo de probabilidad de mutación;
g) añadir la solución de menor error Ek apartada en el paso d) a las N-1 soluciones anteriores;
h) repetir los pasos c) a g) hasta cumplir una condición de parada predefinida.
3.- Método según la reivindicación 2, caracterizado por que el algoritmo de probabilidad de cruce comprende:
i) tomar las N-1 soluciones de dos en dos;
ii) establecer una probabilidad de cruce entre 0 y 1;
iii) generar un número aleatorio entre 0 y 1;
iv) si el número aleatorio generado es mayor que la probabilidad de cruce, no hay cruce;
v) si el número aleatorio generado es menor o igual que la probabilidad de cruce, se cruza parte de una solución con parte de la otra solución de tal forma que se mantiene la longitud de la cadena de caracteres.
4.- Método según la reivindicación 2, caracterizado por que el algoritmo de probabilidad de mutación comprende:
i) tomar las N-1 soluciones de una en una;
ii) establecer una probabilidad de mutación entre 0 y 1;
iii) generar un número aleatorio entre 0 y 1;
iv) si el número aleatorio generado es mayor que la probabilidad de mutación, no hay mutación;
v) si el número aleatorio generado es menor o igual que la probabilidad de mutación, se muta un carácter de la cadena de caracteres de tal forma que se mantiene la longitud de la cadena de caracteres.
5.- Método según la reivindicación 2, caracterizado por que la condición de parada predefinida es al menos una de las siguientes condiciones:
máximo número de iteraciones;
convergencia: no mejora en un número "p" de iteraciones;
estar cerca de un óptimo teórico.
6.- Método según la reivindicación 2, caracterizado por que la función de fitness es una de las siguientes funciones:
mínimos cuadrados;
error medio;
error máximo;
error cuadrático medio;
desviación absoluta media.
7.- Método según la reivindicación 2, caracterizado por que la solución GL(k + 1) tiene la siguiente expresión:
GL(k + 1) = f(P,E,k,SI,IG,PG,CI,M,IC,IP,DI,OC, TI,FV, VI,PC, TE,FA,G(),C(), IS(), IL(),F(),E(-),Z)
donde el operador representa cualquier instante actual o anterior en el tiempo y donde fes una función que se calcula mediante una gramática BNF que comprende la siguiente forma:
<f> ;;= <f><OP><f>
| (<f><OP><f>)
| <PREOP>(<f>)
| <V>
I <Z>
<OP> ::= +
I*
<PREOP> ::= SIN
ICOS
|EXP
|TAN
|LOG
|ABS
LN
TANH
COSH
SENH
DERIVADA_CON_RESPECTO_AL_TIEMPO DERIVADA_CUADRADO_CON_RESPECTO_AL_TIEMPO DERIVADA_TERCERA_CON_RESPECTO_AL_TIEMPO <V> ::= <P>
<A>
#{k}
<SI>
<IG>
<PG>
<CI>
<M>
<IC>
<IP>
<DI>
<OC>
<TI>
<FV>
<VI>
<PC>
<TE>
<FA>
#{G[k-<J>]}
#{C[k-<J>]}
#{IS[k-<J>]}
#{IL[k-<J>]}
#{F[k-<J>]}
#{E[k-<J>]}
#<Z>
<P> ::= "el peso del individuo en kg.";
<E> ::= "edad del individuo en años";
<SI> ::= "unidades de glucemia que baja 1 unidad de insulina en mg/dl";
<IG> ::= "índice glucémico de la ingesta" (el de la glucosa es 1, y puede ser mayor o menor;)
<PG> ::= <D>.<D>
<CI> ::= <D>.<D>
<M> ::= 0
<IC> ::= 5
<IP> ::= 0
<DI> ::= 2
<OC> ::= 3
<TI> ::= 12
<FV> ::= 0.2
<VI> ::= 0.8
<PC> ::= 0.6
<FTSI> ::= +<D> <D>
|-<D>.<D>
<J> ::= 0 |1 |2 |3
| "instantes de tiempo" (por ejemplo: 96 24 horas a intervalos de 15 minutos = 96 instantes de tiempo. En el caso de usar otro horizonte de predicción u otro periodo de muestreo habría que modificar esta regla);
<Z> ::= <D>.<D>
<D> ::= 0 |1 |2 |3 |4 |5 |6
|7
|8
|9
donde los distintos parámetros de entrada son:
P: peso actual en kg;
A: edad actual en años; k: instante actual;
FSI: sensibilidad a la insulina o mg/dl que baja la glucemia por unidad de insulina;
IG: es el índice glucémico;
PG: unidades proteína/grasa: cantidad de alimento que aporta 100Kcal en forma de grasa y/o proteínas, se mide en unidades;
CI: ratio Hidratos de carbono / insulina;
M: menstruación , Sí =1 ó no=0;
IC: insulina Circulante, unidades de insulina;
IP: intervalo entre comienzo de la infusión de insulina prandial y comienzo de la ingesta, en intervalos de 15 minutos;
DI: tiempo de duración de la última ingesta en intervalos de 15 minutos;
OC: orden en que se consumen los alimentos; (número natural correspondiente a una fila en una tabla de posibles ordenaciones)
TI: tiempo desde la última ingesta en intervalos de 15 minutos;
FV: factor de variabilidad de absorción, valor entre 0 y 1;
VI: variabilidad de la insulina, valor entre 0 y 1;
PC: preparación de la comida (fritos, asados, condimentos..), valor entre 0 y 1;
FTSI: factor transitorio de sensibilidad a la insulina: valor de -1 a 1;
Z: es una constante; en cuanto a históricos:
G( ) es el histórico de la glucemia (o parte de él);
C() es el histórico de carbohidratos;
IS() es la insulina de acción corta;
IL() es la insulina de acción larga;
F() es el ejercicio físico; y,
E() es el nivel de estrés.
8.- Método según la reivindicación 2, caracterizado por que la función de mapeo comprende la siguiente expresión:
Choicei = (CIV)MOD (# of choícesf)
donde Choicei es la elección seleccionada para el no-terminal i, CIV es el codón que 5 estamos decodificando, MOD es la función módulo y (# of choicesi) es el número de opciones posibles para la regla en el terminal i.
9.- Método según la reivindicación 1, caracterizado por que el método, entre los pasos i) y ii), opcionalmente comprende evaluar la función GL de predicción de la glucosa
anteriormente calculada cuando existe un modelo de glucosa anteriormente calculado.
10.- Programa de ordenador caracterizado por que comprende la ejecución de un método definido de acuerdo con una cualquiera de las reivindicaciones 1 a 9.
11.- Medio de almacenamiento caracterizado por que comprende un programa de
ordenador definido según la reivindicación 10.
12.- Sistema computacional caracterizado por que en dicho sistema computacional se carga el programa de ordenador definido en la reivindicación 10.
Patentes similares o relacionadas:
Sistemas y métodos para tratar, diagnosticar y predecir la aparición de una afección médica, del 15 de Julio de 2020, de Fundação D. Anna Sommer Champalimaud E Dr. Carlos Montez Champalimaud: Aparato para evaluar si es probable que un paciente tenga un estadio patológico favorable de cáncer de próstata, el aparato comprende: (a) un dispositivo de obtención […]
Dispositivo de procesamiento de datos para el procesamiento de valores de medición, del 22 de Abril de 2020, de F. HOFFMANN-LA ROCHE AG: Dispositivo de procesamiento de datos para el procesamiento de valores de medición de un equipo de medición médico, con una unidad de entrada , una […]
Sistema de análisis apuntador de acontecimientos y de gestión de medicación, del 30 de Octubre de 2019, de CAREFUSION 303, INC: Un método para reducir el riesgo de errores de medicación, el método comprende las etapas de: recibir en un dispositivo móvil un primer valor de un parámetro […]
Sistema y método de visualización en 2D y 3D para la inspección de un tubo de horno, del 11 de Septiembre de 2019, de Quest Integrity USA, LLC: Un sistema para la visualización de datos de inspección recogidos de un horno con una geometría física especificada, en donde dicho horno comprende […]
 Reconocimiento anatómico y análisis dimensional para asistir en la cirugía de mama, del 25 de Julio de 2019, de ALLERGAN, INC.: Método implementado por ordenador de determinación de mediciones de la mama de manera automática a partir de una representación tridimensional (3-D) de la parte superior […]
Reconocimiento anatómico y análisis dimensional para asistir en la cirugía de mama, del 25 de Julio de 2019, de ALLERGAN, INC.: Método implementado por ordenador de determinación de mediciones de la mama de manera automática a partir de una representación tridimensional (3-D) de la parte superior […]
Sistemas y métodos para tratar, diagnosticar y predecir la aparición de una afección médica, del 24 de Julio de 2019, de Fundação D. Anna Sommer Champalimaud E Dr. Carlos Montez Champalimaud: Un aparato para evaluar un riesgo de fallo clínico en un paciente después de que el paciente se haya sometido a una prostatectomía radical, y el aparato […]
 Aparato médico controlado remotamente, del 24 de Julio de 2019, de GAMBRO LUNDIA AB: Una unidad de diálisis adaptada para tratar la sangre de un paciente (P) según una terapia prescrita, la unidad de diálisis presenta una interfaz inalámbrica […]
Aparato médico controlado remotamente, del 24 de Julio de 2019, de GAMBRO LUNDIA AB: Una unidad de diálisis adaptada para tratar la sangre de un paciente (P) según una terapia prescrita, la unidad de diálisis presenta una interfaz inalámbrica […]
Interfaces de usuario gráficas (IUG), procedimientos y aparato para la presentación de datos, del 10 de Julio de 2019, de DUNE MEDICAL DEVICES LTD.: Un sistema de análisis de sustrato, comprendiendo el sistema: (a) una sonda que está configurada y operable para explorar un sustrato y determinar uno o más parámetros […]