MÉTODO BIMODAL PARA CUANTIFICAR PROPIEDADES NO TOPOGRÁFICAS EN MICROSCOPÍA DE FUERZAS.
Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas,
basado en modular en frecuencia y de forma simultánea al menos dos modos de vibración de la micropalanca de un microscopio, que emplea los desplazamientos de frecuencia de los modos excitados y los cambios en la fuerzas de excitación para cuantificar propiedades nanomecánicas.
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P201330281.
Solicitante: CONSEJO SUPERIOR DE INVESTIGACIONES CIENTIFICAS (CSIC).
Nacionalidad solicitante: España.
Inventor/es: GARCIA GARCIA,RICARDO, TOMAS HERRUZO,Elena.
Fecha de Publicación: .
Clasificación Internacional de Patentes:
- G01Q60/32 FISICA. › G01 METROLOGIA; ENSAYOS. › G01Q TECNICAS O APARATOS DE SONDA DE BARRIDO; APLICACIONES DE TECNICAS DE SONDA DE BARRIDO, p. ej. MICROSCOPIA POR SONDA DE BARRIDO [SMP]. › G01Q 60/00 Tipos particulares de microscopía por sonda de barrido [SPM] o aparatos empleados; Componentes esenciales al efecto. › Modo AC.
Fragmento de la descripción:
MÉTODO BIMODAL PARA CUANTIFICAR PROPIEDADES NO TOPOGRÁFICAS EN MICROSCopiA DE FUERZAS
OBJETO DE LA INVENCiÓN
La presente invención se refiere a un método de utilización de un microscopio de fuerzas mediante modulación de frecuencia, excitando simultáneamente al menos dos modos de vibración de la micropalanca, siendo uno de ellos el modo principal que permite seguir la topografía y siendo el otro el modo secundario, caracterizado por una frecuencia más elevada que la del modo principal. Se utiliza cálculo fraccional para relacionar parámetros medidos directamente con el microscopio con las propiedades de las muestras. Se emplean los desplazamientos de frecuencia de los modos excitados y los cambios en la fuerzas de excitación para cuantificar propiedades nanomecánicas de una muestra a medir.
Este método permite calcular diversas propiedades cuantitativas no topográficas de los materiales, utilizando para ello modos de vibración dinámicos sin hacer hipótesis acerca de la indentación de la punta de la micropalanca en la muestra a analizar. Este método puede aplicarse en tiempo real durante la medición, o posteriormente a la obtención de los parámetros directamente medidos en la muestra.
El presente método bimodal para cuantificar propiedades no topográficas en microscopia de fuerzas encuentra aplicación en el ámbito de la investigación científica, mediante microscopía de fuerzas, de todo tipo de materiales, orgánicos e inorgánicos, estando la muestra inmersa en un medio, liquido, gaseoso, o bien en el vacio.
PROBLEMA TÉCNICO A RESOLVER Y ANTECEDENTES DE LA INVENCiÓN
La habilidad de la microscopía de fuerzas para la adquisición de imágenes de un amplio rango de materiales la han convertido en una de las técnicas relevantes para la caracterización de propiedades a escala nanométrica. Como consecuencia de su gran resolución (lateral y vertical) , los microscopios de fuerza atómica (AFM, por las siglas en inglés de Microscopia de Fuerza Alómica) . Se han inlroducido lanlo en laboralorios de investigación como en departamentos de control de calidad en diversos sectores industriales (microelectrónica, polimeros) .
Un microscopio de fuerzas puede operar tanto en modos estáticos como dinámicos. Uno de los métodos que pueden ser utilizados para la determinación cuantitativa de propiedades son los experimentos de nanoindentación, que se caracterizan por su lentitud, la elevada área de contacto y no controlar la fuerza aplicada. Los métodos estáticos están basados en la adquisición de curvas de fuerza de forma simultánea con la adquisición de la imagen topográfica (force volume) . Estos métodos funcionan a frecuencias bajas (1-2 Hz) lo cual implica que un mapa completo requiera tiempos de adquisición de horas. Además, la resolución lateral de estos mapas es pequeña. El método de la fuerza pulsada (A. RosaZeiser, E. Weilandt, S. Hild y O. Marti. The simultaneous measurement of elastie, eleetrostatie and adhesive properties by seanning force mieroseopy: pu/sed-foree mode operation. Measurement Science and Technology 8 (11) , 1333 (1997) ) hace oscilar el piezoeléctrico que mueve la muestra en sentido vertical a frecuencias de entre 100 Hz y 2 kHz, lo que permite la determinación de propiedades mecánicas de forma más rápida, aunque la fuerza máxima aplicada es relativamente elevada (de decenas de nN) .
La reciente invención descrita en el documento de patente US 20120131702 A1 , introduce mejoras en la electrónica que han permitido el desarrollo del método 'peak force tapping' capaz de extraer propiedades de forma robusta con indentaciones de al menos 2 nm y es capaz de establecer la máxima fuerza de interacción punta -muestra en el rango pN-nN. Es de notar que aunque el método ha sido verificado sobre multitud de materiales en aire y líquidos, no existen resultados significativos en cuanto a la cuantificación sobre imágenes con alta resolución lateral de nanopartículas o proteínas individuales.
Los modos dinámicos tienen la ventaja de ser generalmente no invasivos y de incrementar la velocidad de adquisición, de tal forma que la información cuantitativa sea simultánea con la imagen de topografía. Además, y más importante, el hecho de operar a frecuencias cercanas de la de resonancia aumenta la sensibilidad del microscopio. Muchos observables, (término que se refiere a magnitudes directamente medidas en el microscopio) como la fase, los cambios de frecuencia o la amplitud de armónicos superiores, pueden ser relacionados con información composicional de la muestra. Sin embargo, la cuantificación de estas propiedades no es inmediata.
Se puede distinguir entre métodos basados en la obtención de la fuerza de interacción punta -muestra a partir de la deflexión, y métodos paramétricos. En los documentos de patente US 746583 81 Y US 7404314 82, asi como en el articulo: M. Stark, C. Moller, D. J. Müller y
R. Guekenberger. From images to interaetions: High-resolution phase imaging in tappingmode atomic force mieroscopy. Biophysieal Journal 80, 3009-3018 (2001 J, se introducen métodos que reconstruyen el comportamiento de la fuerza de interacción punta -muestra frente al tiempo, para cada pixel de la imagen obtenida mediante microscopía, métodos que permiten obtener el Módulo de Young efectivo, E eft. y otras propiedades de la muestra a la vez que permiten observar si existen fuerzas que no han sido consideradas en el modelo que incrementan el error en la cuantificación. En particular, el método de Sahin (como en la patente US 7404314 82) permite estimar el Módulo de Young efectivo. E". tras una estimación de la indentación basada en la máxima resolución lateral obtenida en la imagen. Entre los métodos paramétricos destaca el trabajo de Raman (A. Raman, S. Trigueros, A. Cartagena, A. P. Z. Stevenson, M. Susilo, E. Nauman adn S. Antoranz Contera, Mapping nanomechanical properties of Uve cells using mu/ti-harmonic atomic force microscopy , Nature Nanotechnology 6, 809-814 (2011» que describe la relación entre el Módulo de Young y distintos componentes harmónicos de la oscilación.
Es de notar que para aumentar la precisión en la medida de propiedades mediante modos dinámicos se debe minimizar el número de hipótesis empleadas. La mayoría de los métodos anteriores efectúan ciertas hipótesis sobre la indentación, como suponer que el radio de contacto es equivalente a la resolución lateral obtenida en la imagen. El radio de contacto real se relaciona con la indentación y el radio de la punta a través de la fórmula re = .Jindentación.jRpunta En general, un cambio en una propiedad física se manifiesta en un cambio en los observables y en un cambio en la distancia entre la punta y la muestra (debido a la realimentación topográfica) . De esta forma, si se aumenta el número de ecuaciones que relacionan la fuerza y los observables, también se podrá determinar más propiedades de la muestra como la indentación de la punta de la micropalanca en la muestra.
La presente invención se basa en modos multifrecuencia de microscopía de fuerzas. Documentos pioneros a la presente invención pueden verse en los documentos de patente US 7958563 82 Y US 7921466 82. La microscopía de fuerzas bimodal es un método de microscopía de fuerza que opera excitando simultáneamente dos modos de vibración de la micropalanca (o cantiléver, como es conocida comúnmente en el estado de la técnica) de un microscopio de fuerza atómica. Estos modos pueden ser, por orden de frecuencia de menor a mayor, el primero y el segundo, el primero y el tercero 0, en general, dos cualesquiera. Esta excitación simultánea permite la duplicación de canales de información.
La Figura 1 muestra la forma teórica de los dos primeros modos flexurales (1 y 2) de vibración de una micropalanca rectangular que oscila en aire. La frecuencia del segundo modo es aproximadamente 6 veces mayor que la del primer modo. La Figura 2 muestra la oscilación vertical de una micropalanca cuando se excitan simultáneamente los dos primeros modos de resonancia, siendo la amplitud del segundo modo mucho menor que la amplitud del primer modo. La Figura 3 describe el funcionamiento de un microscopio de fuerzas bajo la excitación de dos modos de vibración operando en modo de modulación en frecuencia, que consta de los pasos de excitar de forma simultánea al menos el modo fundamental de vibración y un modo más alto de la micropalanca del microscopio mientras la micropalanca se desplaza sobre la superficie de la muestra, y que establece una serie de condiciones para cada uno de los modos.
En las condiciones de funcionamiento del microscopio bimodal se satisfacen ciertas condiciones en el virial de la fuerza de interacción (Vrs) y en la energía...
Reivindicaciones:
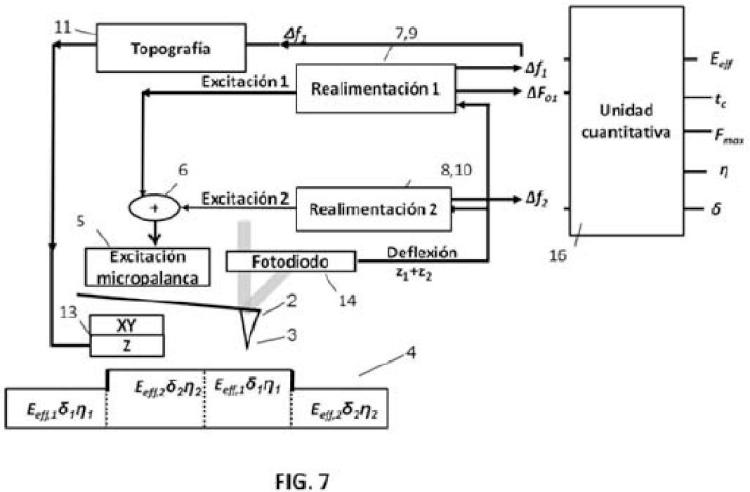
1. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas, basado en modular en frecuencia y de forma simultánea al menos dos modos de vibración de una micropalanca (2) de un microscopio de fuerzas (1) , caracterizado por emplear los desplazamientos de frecuencia de los modos excitados y los cambios en la fuerza de excitación para cuantificar propiedades nanomecánicas.
2. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según la reivindicación 1, caracterizado por que comprende:
a. colocar en la cabeza de un microscopio de fuerzas (1) una micropalanca (2) con una punta (3) en su extremo, que interactúa con la muestra (4) , y que presenta al menos dos modos de vibración, un modo principal y un modo secundario;
b. disponer de dos elementos, uno para hacer vibrar (5) a la micropalanca (2) y el otro para desplazar (13) a la micropalanca (2) sobre la muestra (4) o parte de el la:
c. enviar a la unidad de excitación (5) asociada a la micropalanca (2) de la cabeza del microscopio (1) , las señales de excitación generadas por (7, 8, 9, 10) Y sumar, mediante un sumador de señales (6) , las mencionadas señales de excitación que hacen vibrar a la micropalanca (2) ;
d. calibrar los siguientes parámetros asociados a la operación de la micropalanca (2) :
constante de fuerzas, k;;
factor de calidad, Q ¡;
inversa de la sensibilidad óptica del fotodiodo, i, en cada uno de los dos modos de vibración;
radio, R, de la punta (3) de la micropalanca (2) ;
e) comprobar las hipótesis de partida. según las siguientes etapas:
6.1) comprobar que la amplitud de vibración del modo principal de la micropalanca (2) es mayor que la longitud de escala de la fuerza de interacción.
e.2) comprobar que la amplitud de vibración, del modo secundario de la micropalanca (2) es muy inferior a la amplitud de vibración, del modo principal;
e.3) fijar una pluralidad de bucles de realimentación que comprenden:
-un bucle de realimentación (7) de la amplitud, A1• del modo principal de vibración, donde se hace variar la amplitud de excitación de la micropalanca (2) en dicho modo principal, manteniendo constante dicha amplitud, A1;
-un bucle de realimentación (8) de la amplitud, Az, del modo secundario de vibración, donde se hace variar la amplitud de excitación de la micropalanca (2) en dicho modo secundario, manteniendo constante dicha amplitud, A2;
-un bucle de realimentación (9) , de fase, q¡" del modo principal de vibración, donde se hace variar la frecuencia de excitación, f1 de la micropalanca (2) en dicho modo principal, manteniendo constante la fase, <P1, en un valor igual a TT/2;
-un bucle de realimentación (10) , de fase, <P2, del modo secundario de vibración, donde se hace variar la frecuencia de excitación, h, de la micropalanca (2) en dicho modo secundario, manteniendo constante la fase, <P2, en un valor igual a TT/2;
-un bucle de realimentación (11) responsable de regular la distancia media (12) entre la punta (3) de la micropalanca (2) y la muestra (4) y controlar asi la realimentación topográfica (11) .
f) detectar, mediante un sistema (14) adaptado al efecto, la señal de deflexión de la micropalanca (2) ;
g) registrar, mediante una unidad de procesamiento (15) provista de al menos dos canales de transferencia de información, las señales correspondientes a los modos de vibración, donde dicho registro puede realizarse simultáneamente o posteriormente a la adquisición de una imagen de microscopía;
h) transformar, mediante el empleo de fórmulas analíticas, los datos mostrados en los mapas para métricos de propiedades de la muestra (4) .
3. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según la reivindicación 2, caracterizado por que el sistema punta (3) -micropalanca (2) se sitúa sobre una muestra (4) heterogénea para medir diversas propiedades mecánicas como el Módulo de Young efectivo, EaH• la viscosidad, 11, de la muestra (5) , o la constante de Hamaker, H, de la interfase.
4. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según cualquiera de las reivindicaciones 2 y 3, caracterizado por que en la etapa (c) del método en que se generan las señales de excitación , la micropalanca (2) es excitada según los mencionados modo principal y modo secundario de vibración.
5. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas
según la reivindicación 4, caracterizado por que la señal resultante que llega a la micropalanca (2) viene expresada según la siguiente relación matemática:
(E.?)
donde FOi, fi son, respectivamente, la señal de excitación, y la frecuencia de excitación del modo i que son transferidas al elemento que excita la vibración de la micropalanca (2) .
6. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según la reivindicación 5, caracterizado por que la señal se genera utilizando la señal de referencia de un dispositivo lock-in digital comprendido dentro de un procesador digital de señal.
7. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según cualquiera de las reivindicaciones 2 y 3, caracterizado por que en la etapa (h) del método en que se transforman los datos mostrados en los mapas paramétricos de propiedades de la muestra (4) , se utilizan los cambios en las frecuencias de resonancia del modo principal, 6.f1• y del modo secundario, 6.f2• para hallar el Módulo de Young
efectivo, EeH• de la muestra (4) Y la indentación, é, en función de la posición de la
micropalanca (2) sobre la muestra (4) .
8. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas
según la reivindicación 7, caracterizado por que los datos de cambio en la frecuencia
5 de resonancia del modo principal, 1J.f1• y cambio en la frecuencia de resonancia del
modo secundario, 1J.f2> se convierten, mediante un cálcu lo analítico, y simultáneamente o
posteriormente a la adquisición de una imagen, en mapas paramétricos que expresan el
Módulo de Young efectivo, Eeff, Y la indentación, 15 .
9. Método bimodal para cuantificar propiedades no topográficas según la reivindicación 8,
10 caracterizado por que la fuerza de interacción se modela de acuerdo al modelo de
Hertz y el Módulo de Young efectivo, Eeff, y la indentación, 5, se calculan mediante el
siguiente sistema de ecuaciones:
E = 2J2 k; j, /', ./, ' off W kJ, ' /', .j,
(E.8)
(j = A, kJ, /', .j,
k, j, /', .f, (E.9)
15 10. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas
según la reivindicación 8, caracterizado por que el tiempo de contacto, te, entre la punta
(3) y la muestra (4) se calcula mediante la siguiente expresión matemática:
I =arccos 1--=arccos 1---"I ( 8J I ( k, J, I!.1.J , "1. A, "1. k, 1. I!.j, (E.10)
11. Método bimodal para cuantificar propiedades no topograficas en microscopía de fuerzas
20 según la reivindicación 8, caracterizado por que cuando la punta (3) se encuentra a
una distancia mínima de la muestra (4) , se calcula la fuerza máxima conservativa de
Hertz, Fmax, según la siguiente expresión matemática:
(E. 11 )
28
12. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas
según cualquiera de las reivindicaciones 2, 3 Y 7, caracterizado por que en la etapa (h)
del método en que se transforman los datos mostrados en los mapas paramétricos de
propiedades de la muestra, se utilizan los cambios en las frecuencias de resonancia del
5 modo principal , y del modo secundario, y el cambio en la señal de excitación del modo
principal para hallar la viscosidad, r¡, el módulo de Young efectivo, Eeff, de la muestra (4)
y la indentación, Ó, en función de la posición de la micropalanca (2 ) sobre la muestra
(4) .
13. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas
10 según las reivindicaciones 8, 9 Y 12, caracterizado por que se añade al modelo de la
fuerza conservativa de Hertz una componente disipativa que puede modelarse como
proporcional a la velocidad de indentación, de tal forma que la fuerza total de interacción
se expresa mediante la siguiente relación matemática:
15 donde Ó.r es una función par denominada función de rozamiento generalizado, y 8 es
la velocidad de indentación en la muestra (4) ;
de manera que la inclusión de la mencionada componente disipativa de la fuerza da
lugar a una ecuación adicional para la energía disipada en términos de la semi-integral
de una función, B (d) , relacionada con la fuerza disipativa:
20
!1F (d) = F ( !1J, Cd) + J2ñQ, J, / ''' BCd ) ]1) 1 1) 1 J, k A3/2 -, , ,
(E .13)
donde la función B se define mediante la siguiente expresión matemática:
•
B (x ) =2f!1r (x) dx
(E .14)
29
dando lugar a una ecuación adicional que permite la conversión de las imágenes de 6.k 6.f2 Y F01 en mapas paramétricos del módulo de Young efectivo, Eaf!. de la viscosidad, r, . y de la indentación, (5 , y haciendo que el sistema de tres ecuaciones:
!!.F (d) = F [!!.j, (d) + J2iéQ, j, r y '¡;¡¡¡S' J
01 j, k A3/2 2
, , ,
(E. 17)
con tres incógnitas, Eaf!. 5, 11, se pueda expresar explícitamente, proporcionando además de las ecuaciones para el módulo de Young efectivo, Eaf" Y para la indentación,
15. una ecuación para la viscosidad, r], expresada de la siguiente manera:
k; 41/ (41; /¡Fo, -!1F01¡;2) JTrAIR k, fJz2 Q, 4!;2Fol
(E. 18)
14. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según cualquiera de las reivindicaciones 2 y 3, caracterizado por que la micropalanca (2) opera en régimen atractivo o de no contacto, y la fuerza de interacción entre la punta (3) y la muestra (4) se modela de acuerdo al siguiente modelo matemático, conocido 15 como modelo de Van der Waals:
(E .19) donde d es la distancia entre la punta (3) y la muestra (4) .
15. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según la reivindicación 14, caracterizado por que se calculan analíticamente la semi· derivada y la semi·integral de la fuerza de interacción del modelo de van der Waals, dando lugar a un sistema de dos ecuaciones con dos incógnitas, que se puede expresar explícitamente, proporcionando relaciones para la constante de Hamaker, H, y la distancia mínima, dmin, entre punta (3) y muestra (4) :
(E.20)
3A, k, j, !;j,
k, j!;f,
(E.21 )
16. Método bimodal para cuantificar propiedades no topográficas en microscopia de fuerzas según la reivindicación 15, caracterizado por que la distancia media (12) entre la punta (3) y la muestra (4) se controla manteniendo un cambio en la frecuencia, 6.f1• fijo mientras la micrapalanca (2) se desplaza a lo largo y ancho de la muestra (4) .
17. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas 10 según la reivindicación 15, caracterizado por que la distancia media (12) entre la punta (3) y la muestra (4) se controla manteniendo una fuerza de excitación , F01 , fija.
18. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según la reivindicación 2, caracterizado por que en la etapa e3) se establece el sistema de realimentación (11) topográfico del quinto bucle en otros parámetros como el tiempo 15 de contacto, te, o la fuerza máxima, Fma x, en valores pre-establecidos alternativas al
cambio de frecuencia de resonancia, .ó.f1, o disipación, .ó.F01 .
19. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según la reivindicación 18, caracterizado por que se utiliza realimentación en tiempo de contacto, te, para efectuar medidas no invasivas en materiales blandos.
20. Método bimodal para cuantificar propiedades, según las reivindicaciones 1 y 2, caracterizado por que las fuerzas de interacción entre la punta (3) y la muestra (4) se modelan mediante dos parámetros además de la separación entre la punta y la muestra, de manera que se añade una nueva ecuación que se obtiene al excitar un modo adicional de vibración, n, y registrando como canal adicional, .ó.fn, para tener tres observables conservativos, siendo éstos los cambios de frecuencia de cada modo de vibración , de manera que se obtiene un sistema de tres ecuaciones con tres incógnitas del que extraer las propiedades de la muestra, donde por observables se entiende los parámetros medidos directamente por el microscopio de fuerzas bimodal.
21. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas, según las reivindicaciones 1 y 2, caracterizado por que las fuerzas de interacción entre la punta (3) y la muestra (4) se modelan mediante dos parámetros además de la separación entre la punta y la muestra, de manera que la ecuación adicional se halla registrando la amplitud Bm de un armónico superior, m, del modo principal con frecuencia m il. para tener tres observables que dan lugar a un sistema de tres ecuaciones con tres incógnitas del que extraer las propiedades de la muestra (4) , donde por un armónico superior, Bm. del modo principal se entiende un múltiplo entero de la frecuencia de resonancia de dicho modo principal, y donde los tres observables mencionados son: cambio de frecuencia del modo principal y del modo secundario, bof1, flfz, Y amplitud, Bm, del armónico superior, m,
!J.B, (d) = 2 (J~' F (d) -+r:"F (d» )
3k J 21CA, ' (E.22)
donde 1~'2 F (d) es la integral 3/2 de la fuerza de interacción y 8z es la amplitud del segundo armónico.
. Método bimodal para cuantificar propiedades no topográficas según la reivindicación 13, caracterizado por que la fuerza de interacción contiene una componente disipativa dependiente de dos parámetros y se registra de forma adicional el canal disipación del modo secundario de vibración para utilizar la ecuación que relaciona la energía disipada por el modo secundario con la semi~integral de la función r (d) :
I!.F., (d) = F" (I!.f, (d) + &Q, f, I~"tll' (d) J
!, k, JA,
(E.23)
dando lugar a una ecuación adicional que permite la transformación de las imágenes de flf" bofz, F01 y Foz en observables que aparecen en un sistema de cuatro ecuaciones para hallar simultáneamente la viscosidad, r" y la histéresis de la energía superficial, flEadh .
23. Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas según cualesquiera de las reivindicaciones anteriores, caracterizado por que la medida se realiza teniendo la muestra inmersa en líquido.
Patentes similares o relacionadas:
 MÉTODO BIMODAL PARA CUANTIFICAR PROPIEDADES NO TOPOGRÁFICAS EN MICROSCOPÍA DE FUERZAS, del 4 de Septiembre de 2014, de CONSEJO SUPERIOR DE INVESTIGACIONES CIENTIFICAS (CSIC): Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas, basado en modular en frecuencia y de forma simultánea al menos dos modos de […]
MÉTODO BIMODAL PARA CUANTIFICAR PROPIEDADES NO TOPOGRÁFICAS EN MICROSCOPÍA DE FUERZAS, del 4 de Septiembre de 2014, de CONSEJO SUPERIOR DE INVESTIGACIONES CIENTIFICAS (CSIC): Método bimodal para cuantificar propiedades no topográficas en microscopía de fuerzas, basado en modular en frecuencia y de forma simultánea al menos dos modos de […]
 Microscopio de sonda de barrido con accionador controlado por corriente, del 1 de Marzo de 2013, de SPECS ZURICH GMBH: Un microscopio de sonda de barrido que comprende
una sonda ,
un accionador piezoeléctrico para hacer oscilar la sonda ,
un amplificador invertido […]
Microscopio de sonda de barrido con accionador controlado por corriente, del 1 de Marzo de 2013, de SPECS ZURICH GMBH: Un microscopio de sonda de barrido que comprende
una sonda ,
un accionador piezoeléctrico para hacer oscilar la sonda ,
un amplificador invertido […]