Simulador de producción para simular un campo de hidrocarburos maduro.
Simulador de producción que implementa leyes de física de yacimiento aptas para simular un campo de hidrocarburos maduro,
que proporciona cantidades producidas por fase, por pozo, por capa o grupo de capas y por tiempo en función de parámetros de producción, en el que dicho simulador de producción es definido por un conjunto de parámetros a dentro de un espacio de soluciones candidatas a simulador de producción, establece una correspondencia con datos históricos de dicho campo de hidrocarburos maduro y presenta una fiabilidad de pronóstico que puede caracterizarse, según la teoría de aprendizaje estadístico, por el riesgo esperado de pronóstico R(a) asociado con dichos parámetros a, en el que dicho espacio de soluciones candidatas a simulador de producción para convertirse en un simulador de producción del campo de hidrocarburos, es la combinación de la física de transferencia de pozo y la física de propagación del yacimiento, estando cada una de dichas soluciones candidatas a simulador de producción asociada con y definida por un conjunto de dichos parámetros a, definiendo estos parámetros a la solución candidata a simulador de producción que relacionará los parámetros de producción de entrada PPktc con las cantidades producidas Qjktc.
Tipo: Patente Internacional (Tratado de Cooperación de Patentes). Resumen de patente/invención. Número de Solicitud: PCT/EP2011/059968.
Solicitante: Foroil.
Nacionalidad solicitante: Francia.
Dirección: 10 RUE LINCOLN 75008 PARIS FRANCIA.
Inventor/es: OURY,JEAN-MARC, HEINTZ,BRUNO, DE SAINT GERMAIN,HUGUES.
Fecha de Publicación: .
Clasificación Internacional de Patentes:
- G01V1/00 FISICA. › G01 METROLOGIA; ENSAYOS. › G01V GEOFISICA; MEDIDA DE LA GRAVITACION; DETECCION DE MASAS U OBJETOS; MARCAS O ETIQUETAS DE IDENTIFICACION (medios para indicar dónde se encuentran personas sepultadas accidentalmente, p. ej. por la nieve A63B 29/02). › Sismología; Prospección o detección sísmica o acústica.
PDF original: ES-2532766_T3.pdf
Fragmento de la descripción:
Simulador de producción para simular un campo de hidrocarburos maduro.
El campo técnico de la invención es la explotación de campos de hidrocarburos. Más particularmente, la invención se refiere a un procedimiento de construcción de un simulador fiable que pueda pronosticar cantidades producidas frente a parámetros de producción, en el caso particular de los campos maduros.
Los campos de hidrocarburos maduros representan un desafío especial tanto en cuanto a la inversión como a la asignación de recursos humanos, porque el valor neto actual de cualquier nueva inversión disminuye con el grado de madurez. Por tanto, puede invertirse cada vez menos tiempo y esfuerzo en estudios de yacimiento para dar soporte a la explotación del campo. Aun así, sigue habiendo oportunidades para mejorar la producción a lo largo de un denominado comportamiento de línea de base o de explotación normal de un campo maduro completo, incluso con poca inversión. En el pasado, las opciones estratégicas con vistas a gestionar el campo de hidrocarburos crearon cierta heterogeneidad en presión y saturación. Éstas pueden reconsiderarse drásticamente y los parámetros de producción pueden reorganizarse de manera correspondiente. Con respecto a un campo de hidrocarburos maduro, en el pasado se exploraron muchas vías de producción, y puede aplicarse un proceso de aprendizaje: pueden implementarse parámetros reorganizados con un bajo riesgo.
Se conocen actualmente dos enfoques de la técnica anterior para modelar el comportamiento de un campo de hidrocarburos y pronosticar una cantidad esperada producida en respuesta a un conjunto dado de parámetros de producción aplicados.
Un primer enfoque, denominado modelo en malla o modelado de elementos finitos divide un yacimiento en más de cientos de miles de elementos (celdas, líneas de flujo...), incluyendo cada celda varios parámetros (permeabilidad, porosidad, saturación inicial...), y aplica leyes físicas a cada una de dichas celdas con el fin de modelar el comportamiento de fluidos en el campo de hidrocarburos. En ese caso, la denominada dimensión VC, de Vapnik-Chervonenkis, h del espacio de soluciones S, del que se selecciona el simulador, es muy grande. Por tanto, el número m disponible de datos medidos en los datos históricos sigue siendo relativamente pequeño, incluso para
h_
campos maduros, y la razón Aparece ser muy grande en comparación con 1. Como resultado de la teoría de aprendizaje de Vapnik, que se menciona en más detalle más adelante, el riesgo esperado de pronóstico R no está delimitado apropiadamente (debido al término <6), y un simulador de este tipo no puede considerarse fiable, incluso aunque presente una correspondencia muy buena con los datos históricos. En la práctica, está ampliamente reconocido que para tales modelos en malla, una buena correspondencia con el historial no garantiza un buen pronóstico: existen billones de formas de establecer una correspondencia con el pasado, lo que deja una gran incertidumbre sobre cuál proporciona un buen pronóstico.
Un segundo enfoque, en cambio, utiliza modelos simplificados en exceso, tales como, por ejemplo, curvas de declinación o balance de materia. Sin embargo, esto está demasiado simplificado para tener en cuenta apropiadamente la física y la geología relevante del yacimiento, en particular fenómenos e interacción compleja. En tal caso, el riesgo esperado de pronóstico R no se minimiza, porque no puede alcanzarse una buena correspondencia (el término de riesgo empírico Remp sigue siendo grande).
En resumen, la invención representa un buen compromiso entre enfoques de modelado demasiado complejos y demasiado simplistas. Sólo es válido para campos maduros, que proporcionan suficiente información del pasado, en forma de datos históricos, HD, para permitir construir un espacio S de candidatos para llegar a ser un simulador de producción de campo suficientemente grande como para tener en cuenta todos los fenómenos clave implicados en el campo, sin volverse demasiado complejo y por tanto requerir calibrar demasiados datos históricos.
La teoría de aprendizaje estadístico de Vapnik define en qué condiciones puede concebirse un simulador de este tipo. Un simulador de este tipo puede diseñarse de tal manera que cumpla con las condiciones para una capacidad de pronóstico fiable.
El objeto de la invención es un simulador de producción, para simular un campo de hidrocarburos maduro, que proporcione la cantidad producida por fase, por pozo, por capa (o grupo de capas) y por tiempo en función de parámetros de producción, en el que dicho simulador de producción establece una correspondencia suficientemente buena con datos históricos de dicho campo de hidrocarburos maduro y verifica una condición de Vapnik. Dicha condición de Vapnik garantiza que las cantidades que se ha calculado que van a producirse por fase, por pozo, por capa (o grupo de capas) y por tiempo sean precisas. Esto permitirá a los usuarios de este simulador reproducir diferentes escenarios de producción, según diferentes parámetros de producción, proporcionando cada uno de ellos cantidades fiables, de modo que tales escenarios puedan compararse correctamente entre sí y pueda seleccionarse uno apropiado según criterios específicos. Como todos los escenarios de producción proporcionarán cantidades fiables, el seleccionado también proporcionará un pronóstico fiable de la producción y, por tanto, se convertirá en una vía preferida y de bajo riesgo para la producción del campo.
Según otra característica de la invención, se obtiene una correspondencia con datos históricos cuando:
«feM/DlIjr-, _Xy;r, |
\k
-Xy r,i
para más del p% de valores Q^hd existentes y el petróleo acumulado producido en el
mismo intervalo de tiempo [T-i-Xy, T-i] es preciso hasta £2, donde
Qpktb son cantidades producidas por fase, por pozo, por capa (o grupo de capas) y por tiempo, determinadas por el simulador de producción,
QqktbHD son las mismas cantidades producidas por fase, por pozo, por capa (o grupo de capas) y por tiempo, encontradas en los datos históricos,
[TrXy, T-i] es el intervalo de tiempo que comprende los X años más recientes antes del tiempo T-i, siendo Ti la última fecha para la que hay disponibles datos históricos,
Z L , indica una norma de Z en el intervalo de tiempo [Ti,T2],
II W[Tl,T2\
siendo ei un número positivo pequeño con respecto a 1, y
siendo e2 un número positivo pequeño con respecto a 1, y siendo p un número positivo próximo al 1%.
Tal característica permite definir en la práctica la situación en la que un simulador puede considerarse como que proporciona una correspondencia satisfactoria con el historial, que es una condición necesaria para ser un candidato para presentar capacidades de pronóstico satisfactorias.
Según otra característica de la invención, X = 5, e1 = ,2 y e2 = ,15 y p = 9%.
Tal característica permite formular las condiciones en las que la correspondencia con el historial puede considerarse precisa; da un orden de magnitud de la precisión que puede esperarse para cantidades pronosticadas satisfactorias.
Según otra característica de la invención, la condición de Vapnik se expresa como m donde: h es la dimensión de Vapnik-Chervonenkis del espacio S de soluciones, del que se selecciona el simulador, y m es el número de medidas independientes disponibles en los datos históricos.
Tal característica permite formular las condiciones en las que pueden calcularse para conseguir una capacidad de pronóstico satisfactoria.
Según otra característica de la invención, la condición de Vapnik se verifica realizando una prueba ciega satisfactoria a lo largo de N años, según se define mediante las etapas siguientes:
- determinar un simulador de producción que establece una correspondencia con datos históricos a lo largo de un intervalo de tiempo que precede a T-Ny,
- pronosticar cantidades producidas a lo largo de un intervalo de tiempo [T-Ny, T], dados unos parámetros de producción en el mismo intervalo de tiempo [T-Ny, T],
- siendo la prueba ciega satisfactoria cuando:
la
I----Ü'
II «*'*«o||[r_,vv.i7| para más del p% de valores Q<pktbHD existentes y el petróleo acumulado producido en el
mismo intervalo de tiempo [T-Ny, T| es preciso hasta e2, donde
Qcpwb son cantidades producidas por fase, por pozo, por capa (o grupo de capas) y por tiempo, determinadas por el simulador de producción,
QqktbHD son las mismas cantidades producidas por fase, por pozo, por capa (o grupo de capas) y por tiempo, encontradas en los datos históricos,
[T-Ny, T| es... [Seguir leyendo]
Reivindicaciones:
1. Simulador de producción que ¡mplementa leyes de física de yacimiento aptas para simular un campo de hidrocarburos maduro, que proporciona cantidades producidas por fase, por pozo, por capa o grupo de capas y por tiempo en fundón de parámetros de producción, en el que dicho simulador de producción es definido por un conjunto de parámetros a dentro de un espacio de soluciones candidatas a simulador de producción, establece una correspondencia con datos históricos de dicho campo de hidrocarburos maduro y presenta una fiabilidad de pronóstico que puede caracterizarse, según la teoría de aprendizaje estadístico, por el riesgo esperado de pronóstico Ría) asociado con dichos parámetros a, en el que dicho espacio de soluciones candidatas a simulador de producción para convertirse en un simulador de producción del campo de hidrocarburos, es la combinación de la física de transferencia de pozo y la física de propagación del yacimiento, estando cada una de dichas soluciones candidatas a simulador de producción asociada con y definida por un conjunto de dichos parámetros definiendo estos parámetros a la solución candidata a simulador de producción que relacionará los parámetros de producción de entrada PPktc con las cantidades producidas Q(Pmc.
2. Simulador de producción según la reivindicación 1, definido por un conjunto de parámetros a dentro de un espacio de soluciones candidatas a simulador de producción, que puede demostrar un riesgo esperado de pronóstico R(a).
minimizando una condición de contorno
KJ
que se deriva de la desigualdad de Vapnik:
/
\
R(a) es el riesgo esperado de pronóstico asociado con los parámetros a,
Remp{v) es un riesgo empírico asociado con los parámetros a, determinado por un proceso de establecimiento de correspondencia con datos históricos,
8 es un número positivo próximo a cero, definiendo 1-8 una probabilidad que conserva la desigualdad, y <¡> es una función definida por:
| h J | J2 | |
| -,s | = 2J- | |
| {m ) | \ m |
hlog\
2 em
h
MI
w
D
donde
h es la dimensión de Vapnik-Chervonenkis del espacio de soluciones candidatas a simulador de producción
s,y
m es el número de medidas independientes disponibles en los datos históricos, e es igual a exp(1).
3. Simulador de producción según la reivindicación 1, en el que se obtiene una correspondencia con datos históricos cuando:
o*»_ Q i
<pktbliD
fi
[Tj -XyJt]
<pktbHD
ITT.- Xy,Ti 1
J para el p% de los
producido en el mismo intervalo de tiempo [T-i-Xy, T-i] es
valores Q^hd existentes y el petróleo acumulado preciso hasta e2, donde
Q<pkib son cantidades producidas por fase tp, por pozo k, por capa o grupo de capas b y por tiempo t, determinadas por el simulador de producción 2,
Q^tbHD son las mismas cantidades producidas por fase <p, por pozo k, por capa o grupo de capas b y por tiempo t, encontradas en los datos históricos,
[T-i-Xy, Ti] es el intervalo de tiempo que comprende los X años más recientes antes del tiempo Ti, siendo Ti la última fecha para la que hay disponibles datos históricos (HD),
Z L _ i indica una norma de Z en el intervalo de tiempo [Ti,T2],
II UlilJíJ
siendo e-i un número positivo pequeño con respecto a 1, siendo e2 un número positivo pequeño con respecto a 1, y siendo p un número positivo próximo al 1%.
4. Simulador de producción según la reivindicación 3, en el que X = 5, ei = ,2, e2 = ,15 y p = 9%.
-*A,
5. Simulador de producción según la reivindicación 1, en el que la condición de Vapnik se expresa como m donde:
h es la dimensión de Vapnik-Chervonenkis del espacio de soluciones candidatas a simulador de
producción, y
m es el número de medidas independientes disponibles en los datos históricos.
6. Simulador de producción según la reivindicación 1, en el que la condición de Vapnik se verifica realizando una prueba ciega satisfactoria a lo largo de N años, según se define mediante las etapas siguientes:
determinar un simulador de producción estableciendo una correspondencia con los datos históricos a lo largo de un intervalo de tiempo que precede a T-Ny,
pronosticar cantidades producidas en un intervalo de tiempo [T-Ny, 7], dados unos parámetros de producción en el mismo intervalo,
siendo la prueba ciega satisfactoria cuando:
Q
ipktbHD
Ik
[T-Nyj]
L J para el p% de todos los valores Q^kibno, y el petróleo acumulado
producido en el mismo intervalo de tiempo [T-Ny, T] es preciso hasta e2, donde
Qqktb son cantidades producidas por fase cp, por pozo k, por capa o grupo de capas b y por tiempo t, determinadas por el simulador de producción,
QqktbHD son las mismas cantidades producidas por fase <p, por pozo k, por capa o grupo de capas b y por tiempo t, encontradas en los datos históricos,
[T-Ny, T] es el intervalo de tiempo que comprende los N años más recientes antes del tiempo T, siendo T la última fecha para la cual hay disponibles datos históricos HD,
Z
indica una norma de Z en el intervalo de tiempo [Ti,T2],
siendo £i un número positivo pequeño con respecto a 1, siendo e2 un número positivo pequeño con respecto a 1, y siendo p un número próximo al 1%.
7. Simulador de producción según la reivindicación 6, en el que p = 9%, £i = ,1 y £2 = ,1 y N = 3.
8. Simulador de producción según cualquiera de las reivindicaciones 1 a 7, en el que la condición de Vapnik es una
\PP-PP
propiedad de estabilidad de pronóstico verificada cuando si
t II
Qtpkib ~ Qqtdb
H
fox]
I®
- Q®
ipktbHD
fox]
lia
t?o£]
Sí'
entonces
|q»*»1[t j,
H[t.T4-m)>]
^ ne
Wy]
donde
PP son parámetros de producción,
PP son parámetros de producción ligeramente variables,
QcpktbHD son cantidades producidas por fase <p, por pozo k, por capa o grupo de capas b y por tiempo t, encontradas en los datos históricos,
QqktbHD son cantidades ligeramente variables producidas por fase <p, por pozo k, por capa o grupo de capas b y por tiempo t, encontradas en unos datos históricos ligeramente variables,
QtpWí, son cantidades producidas por fase cp, por pozo k, por capa o grupo de capas b y por tiempo t, determinadas por el simulador de producción,
Qpktb son cantidades producidas por fase cp, por pozo k, por capa o grupo de capas b y por tiempo t, determinadas por otro simulador de producción suficientemente próximo determinado a partir de datos históricos ligeramente variables,
[To, T] es el intervalo de tiempo desde el tiempo T hasta el tiempo T, que son respectivamente la fecha inicial y la última fecha para la que hay disponibles datos históricos,
[T, T+Ny] es el intervalo de tiempo que comprende los N años después del tiempo T,
Z r , indica una norma de Z en el intervalo de tiempo [T-i,T2],
siendo e un número positivo pequeño con respecto a 1, y siendo n un número entero pequeño inferior a 5.
9. Simulador de producción según la reivindicación 8, en el que e = ,5, n = 2 y N = 3.
1. Simulador de producción según la reivindicación 1, construido siguiendo las etapas siguientes:
definir una partición de yacimiento inicial detallada, propiedades de roca, leyes de física de yacimiento y leyes de física de pozo,
aumentar a escala dicha partición de yacimiento, propiedades de roca, leyes de física de yacimiento y leyes de física de pozo hasta que se verifique dicha condición de Vapnik, y
optimizar dicho simulador de producción seleccionando de entre las soluciones candidatas a simulador de producción, la solución candidata a simulador de producción que minimiza un riesgo esperado de pronóstico R(a).
11. Simulador según la reivindicación 1, en el que dicha partición de yacimiento se aumenta a escala siguiendo las etapas siguientes:
G-ÚÚG.*
dividir un yacimiento G en unas partes elementales Gah. de manera que «-it-i con Gab n Gab- = para (a,b)£ (a,b), donde ae {1...A} describe un área x-y, y be{1...B} describe una capa z,
agrupar unas partes elementales adyacentes Gab que presentan propiedades de roca homogéneas, en subqeoloqías Gc donde ce{1...C}.
12. Procedimiento según la reivindicación 1, en el que las propiedades de rocas se aumentan a escala siguiendo una etapa de promediado de las propiedades de roca RPr en cada subgeología Gc, según la fórmula:
13. Simulador según la reivindicación 1, en el que las leyes de física de yacimiento se aumentan a escala de tal manera que se apliquen con los parámetros de funcionamiento de la subgeología Gg y en el que escalas de espacio y tiempos asociadas con la subgeología Gg se determinan de tal manera que el espacio de soluciones candidatas a simulador de producción asociado sea coherente con la complejidad de los datos históricos al nivel de pozo.
14. Simulador de producción según la reivindicación 1, construido siguiendo las etapas siguientes:
definir una partición de yacimiento inicial basta, propiedades de roca, leyes de física de yacimiento y leyes de física de pozo,
reducir a escala dicha partición de yacimiento, propiedades de roca, leyes de física de yacimiento y leyes de física de pozo, mientras se mantiene verificada dicha condición de Vapnik, hasta que el simulador de producción establece una correspondencia con datos históricos, y
optimizar dicho simulador de producción seleccionando de entre las soluciones candidatas a simulador de producción, la solución candidata a simulador de producción que minimiza un riesgo esperado de pronóstico Ría).
15. Simulador según la reivindicación 14, en el que dicha partición de yacimiento se reduce a escala siguiendo las etapas siguientes:
partir del yacimiento entero,
16. Simulador según la reivindicación 14, en el que las propiedades de rocas se reducen a escala definiendo nuevas propiedades de roca independientes en cada subgeología Gg.
17. Simulador según la reivindicación 14, en el que las leyes de física de yacimiento se reducen a escala de tal manera que se apliquen con los parámetros de funcionamiento de la subgeología Gg y en el que las escalas de espacio y tiempos asociadas con la subgeología Gg se determinan de tal manera que el espacio de soluciones candidatas a simulador de producción asociado sea coherente con la complejidad de los datos históricos al nivel de
18. Simulador según la reivindicación 1, en el que las leyes de física de yacimiento se derivan de las ecuaciones de (Navier-) Stokes de conservación de momento y conservación de masa para un fluido que evoluciona en una roca modelada como medio poroso sólo caracterizado por su porosidad promediada, permeabilidad y permeabilidad relativa km por fase <g por subgeología c.
19. Simulador según la reivindicación 18, en el que las leyes de física de yacimiento comprenden las fórmulas:
c
donde Vc es el volumen de la subgeología Gc.
dividir dicho yacimiento en subgeologías Gg donde c e{1...C} estando presente una variación sustancial de propiedades alrededor de la frontera entre dichas subgeologías.
pozo.
donde:
í7<pkc es la velocidad de la fase cp en el pozo k, en la subgeología c, es la viscosidad de la fase cp, en la subgeología c, p<pC es la densidad de la fase cp, en la subgeología c,
c es la presión de la fase cp, en la subgeología c, g es el vector de gravedad, k es un coeficiente de permeabilidad, y
/óipc es un coeficiente de permeabilidad relativa de la fase <p, en la subgeología c.
2. Simulador según la reivindicación 19, en el que las leyes de física de yacimiento comprenden además leyes de transferencia de calor entre un fluido o un gas y una roca que vienen dadas por las siguientes fórmulas:
^,(p.s. +p!s!'yv.(pu +p¡u¡)=
4'4(rA)+ v-(aa)=
4 (es + Ef)+ VÍI, - MT)V r)« o,
donde
7 = T(x,y,z) es la temperatura y puede variar en el yacimiento,
O es la porosidad de la roca,
Sp es la saturación de la fase <p, pp es la densidad de la fase cp, u<p es la velocidad de la fase cp,
£ es la energía interna volumétrica (índices s y f correspondientes respectivamente a fases sólida y fluida), Uf= Ug+ U+ Uw es el flujo de entalpia, donde hq es la entalpia específica de la fase cp,
hg = hw + A, siendo A el calor específico de evaporación de agua, siendo los índices g, w, o respectivamente para gas, agua y petróleo,
X (7) es el coeficiente de conductividad del yacimiento.
21. Simulador según la reivindicación 2, en el que las leyes de física de yacimiento comprenden además leyes de fase que vienen dadas por:
IV = v(p-^ la viscosidad de la fase cp en la subgeología c, en función de la presión local P y la temperatura local 7;
Pepe = P*c(P, T) la densidad de la fase cp en la subgeología c, en función de la presión local P y la temperatura local 7;
/V = kr<?c(P,T) el coeficiente de permeabilidad relativa de la fase cp en la subgeología c, en función de la presión local Py la temperatura local 7.
22. Simulador según la reivindicación 1, en el que las leyes de física de pozo comprenden las fórmulas:
Qipktc = Tkc(PPktc,u,pi<c) donde:
Qjp/rfc es la cantidad producida de la fase cp en el pozo k en el tiempo t en la subgeología c,
Tkc es una función de transferencia de pozo k, en la subgeología c,
PPktc son los parámetros de producción aplicados al pozo k en la subgeología c, en el tiempo t,
u^kc es la velocidad de la fase cp en el pozo k en la subgeología c.
23. Simulador para explotar de manera óptima un campo de hidrocarburos maduro, que comprende las etapas siguientes:
construir un simulador de producción según cualquiera de las reivindicaciones anteriores,
iterar varios ciclos de dicho simulador de producción con el fin de encontrar los parámetros de producción óptimos que optimizan un valor de ganancia derivado a partir de dicha cantidad producida,
aplicar dichos parámetros de producción óptimos obtenidos de este modo para explotar el campo de hidrocarburos.
24. Simulador según la reivindicación 23, en el que dicho valor de ganancia optimizado es un valor actual neto o las reservas de dicho campo de hidrocarburos.
25. Simulador según la reivindicación 24, en el que dicho valor actual neto NPV se determina utilizando la fórmula:
2'.-2c.-2S(rcrn<^n,dy
¡ \ k C } +a) i V * k k c / {1 +a)
S,
donde:
Pkc es producción de petróleo (en barriles) para el pozo ky la subgeología c, R¡k es impuestos y regalías para el pozo k y el año i,
S¡ es el precio de venta del petróleo (por barril) para el año i, d es la tasa de descuento porcentual,
/¡k es la inversión realizada en el pozo k durante el año i,
OC¡k son los costes de operación para el pozo k durante el año i,
Lkc es la producción de líquido (en barriles) para el pozo ky la subgeología c, TO¡ es el coste de procesamiento (por barril de petróleo), para el año i.
TL\ es el coste de procesamiento (por barril de líquido), para el año i.
Patentes similares o relacionadas:
SISTEMA Y MÉTODO DE ALERTA DE TIEMPO ESTIMADO DE LLEGADA Y DE INTENSIDAD ESPERADA EN UNA ZONA DETERMINADA, PRODUCTO DE UN MOVIMIENTO SÍSMICO, del 30 de Enero de 2020, de XANCURA SPA: La presente invención se relaciona con un método y sistema de alerta de tiempo estimado de llegada y de intensidad esperada en una zona determinada producto de un movimiento […]
MÉTODO Y SISTEMA DE DETECCIÓN Y CARACTERIZACIÓN DE ONDAS INDUCIDAS POR EL FLUJO DE FLUIDOS, LOS FLUJOS DE PARTÍCULAS ATÓMICAS, LA PROPAGACIÓN DE FRACTURAS Y LA ACTIVACIÓN DE FALLAS GEOLÓGICAS, del 19 de Abril de 2018, de PECH PÉREZ, Andrés: La presente invención, se refiere a un sistema y método constituidos por tres etapas: adquisición, procesado e interpretación; por su generalidad, este método […]
Búsqueda simultánea de fuentes durante la adquisición sísmica y la inversión sísmica, del 4 de Abril de 2018, de EXXONMOBIL UPSTREAM RESEARCH COMPANY: Un procedimiento para deducir un modelo de subsuperficie de velocidad u otra propiedad física, que comprende: obtener datos sísmicos adquiridos en una medición […]
Sistema y procedimiento para detectar la caída de piedras, del 18 de Enero de 2017, de Weir - Jones Engineering Consultants Ltd: Un sistema de detección de caída de piedras en la proximidad de un tramo de vía férrea, comprendiendo el sistema: una pluralidad de […]
Aparato sensor y método para detectar las ondas p generadas por un terremoto y generar una señal de control sensible, del 21 de Enero de 2015, de SEISMIC WARNING SYSTEMS, INC: Aparato para detectar ondas P generadas por terremotos, que comprende: medios que forman un alojamiento adaptado para montarse a una estructura de soporte […]
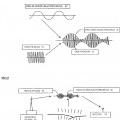 Dispositivo de separación/detección automática de ruido de una onda de radio, del 23 de Julio de 2014, de KUMAGAI, HIDEKI: Un aparato para separar y detectar automáticamente el ruido de ondas de radio generadas como un síntoma premonitorio de terremotos, comprendiendo el aparato:
medios […]
Dispositivo de separación/detección automática de ruido de una onda de radio, del 23 de Julio de 2014, de KUMAGAI, HIDEKI: Un aparato para separar y detectar automáticamente el ruido de ondas de radio generadas como un síntoma premonitorio de terremotos, comprendiendo el aparato:
medios […]
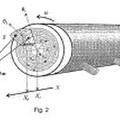 Método de procesamiento y adquisición de señales sísmicas durante la construcción de un túnel, del 14 de Mayo de 2014, de Istituto Nazionale di Oceanografia e di Geofisica Sperimentale - OGS: Método para la adquisición y procesamiento de señales sísmicas durante la perforación de un túnel que comprende las siguientes etapas:
disposición […]
Método de procesamiento y adquisición de señales sísmicas durante la construcción de un túnel, del 14 de Mayo de 2014, de Istituto Nazionale di Oceanografia e di Geofisica Sperimentale - OGS: Método para la adquisición y procesamiento de señales sísmicas durante la perforación de un túnel que comprende las siguientes etapas:
disposición […]
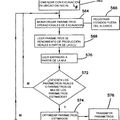 SISTEMA Y PROCEDIMIENTO DE ADQUISICION DE DATOS Y CONTROL DE EXCAVADORA, del 21 de Enero de 2010, de VERMEER MANUFACTURING COMPANY: Un sistema para cartografiar un útil subterráneo, que comprende: una unidad de adquisición de datos geofísicos que genera datos de detección representativos de un […]
SISTEMA Y PROCEDIMIENTO DE ADQUISICION DE DATOS Y CONTROL DE EXCAVADORA, del 21 de Enero de 2010, de VERMEER MANUFACTURING COMPANY: Un sistema para cartografiar un útil subterráneo, que comprende: una unidad de adquisición de datos geofísicos que genera datos de detección representativos de un […]