METODO Y SISTEMA DE SIMULACION MEDIANTE DINAMICA MOLECULAR CON CONTROL DE ESTABILIDAD.
Método y sistema de simulación mediante dinámica molecular con control de estabilidad.
La presente invención tiene su aplicación dentro del campo de dinámica molecular, la cual consiste en métodos de computación para la predicción de la estructura y función de biomoléculas, y en particular de proteínas, mediante la simulación de los procesos de plegamiento de las mismas y de interacción con otras biomoléculas en un solvente. Más particularmente, la invención se refiere a un método y un sistema de control de estabilidad de las simulaciones y de elección del paso de tiempo usado en la integración numérica de las ecuaciones del movimiento. La invención logra reducir el tiempo de simulación de la dinámica molecular mediante la optimización de la elección paso de tiempo a través de un control adaptativo o permitiendo pasos de tiempo mayores corrigiendo las trayectorias en base a un control de la potencia.
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P201231189.
Solicitante: PLEBIOTIC, S.L.
Nacionalidad solicitante: España.
Inventor/es: LOPEZ MEDRANO,ALVARO, CAMPO CAMACHO,ALFONSO, SANCHO SANZ,JAVIER, MARTÍNEZ ABÁN,Roldán, ECHENIQUE ROBBA,Pablo, MARTÍNEZ BENITO,Roberto.
Fecha de Publicación: .
Clasificación Internacional de Patentes:
- G06F17/13 FISICA. › G06 CALCULO; CONTEO. › G06F PROCESAMIENTO ELECTRICO DE DATOS DIGITALES (sistemas de computadores basados en modelos de cálculo específicos G06N). › G06F 17/00 Equipo o métodos de procesamiento de datos o de cálculo digital, especialmente adaptados para funciones específicas (recuperación de la información, estructuras de las bases de datos o estructuras de los sistemas de archivos G06F 16/00). › Ecuaciones diferenciales (utilizando analizadores diferenciales digitales G06F 7/64).
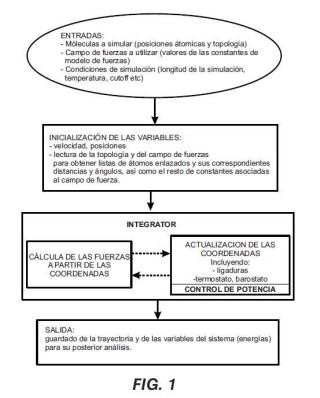
Fragmento de la descripción:
Método y sistema de simulación mediante dinámica molecular con control de estabilidad
Objeto de la invención La presente invención tiene su aplicación dentro del campo de dinámica molecular, la cual consiste en métodos de computación para la predicción de la estructura y función de biomoléculas, y en particular de proteínas, mediante la simulación de los procesos de plegamiento de las mismas y de interacción con otras biomoléculas en un solvente. La Dinámica Molecular también permite simular sistemas más sencillos, como gases o fluidos, siendo la presente invención también aplicable. Más particularmente, la invención que aquí se describe, dentro de la Dinámica Molecular, se refiere a un método de control de estabilidad de las simulaciones y de elección del paso de tiempo usado en la integración numérica de las ecuaciones del movimiento.
El método de la invención se implementa en un ordenador o cualquier equipo electrónico programable adecuado, y aporta el efecto o ventaja de reducir el tiempo de simulación de la Dinámica Molecular mediante la optimización de la elección paso de tiempo a través de un control adaptativo o permitiendo pasos de tiempo mayores corrigiendo las trayectorias en base a un control de la potencia.
Antecedentes de la invención La estructura tridimensional de una proteína determina su función biológica (véase Berg JM, Tymoczko JL, Str y er L., Biochemistr y , 5th edition, W H Freeman, 2002) . Por tanto, es de vital importancia la determinación de dicha estructura para, entre otros, el diseño de fármacos. Una forma de determinar la mencionada estructura es mediante técnicas de cristalización por rayos X o por resonancia magnética nuclear (véase P. Narayanan, Essentials of Biophysics, Second Edition, Anshan Ltd., 2010) . No obstante, éstas técnicas no están exentas de imperfecciones y no permiten con facilidad el proceso opuesto, es decir, la determinación de la cadena de aminoácidos que permite obtener una cierta estructura (véase Tamar Schlick, Molecular Modeling and Simulation: An Interdisciplinar y Guide, Springer, 2006) . Estos hechos, unidos al aumento de la capacidad de procesamiento de los computadores, favorecido el desarrollo, en los últimos años, de la Dinámica Molecular que consiste en la simulación por ordenador del proceso de plegamiento de una proteína o de su interacción con otras moléculas.
Ha sido demostrado (véanse P. L. Freddolino, K. Schulten, Common Structural Transitions in Explicit-Solvent Simulations of Villin Headpiece Folding, Biophysical Journal Volume 97 October 2009 2338–2347, P. L. Freddolino, F. Liu, M. Gruebele, K.Schulten, Ten-Microsecond Molecular Dynamics Simulation of a Fast-Folding WW Domain, Biophysical Journal, Volume 94, Issue 10, L75-L77, 15 May 2008, S. K. Sadiq, G. De Fabritiis, Explicit solvent dynamics and energetics of HIV-1 protease flap-opening and closing, Proteins: Structure, Function, and Bioinformatics Volume 78, Issue 14, pages 2873–2885, 1 November 2010) que, la aproximación mediante la mecánica de Newton, es válida para modelar la dinámica (proceso de plegamiento o de interacción con otras moléculas) de grandes moléculas como las proteínas, la cual es conocida como Dinámica Molecular. Teniendo pues
en cuenta la segunda Ley de Newton y que, en ese caso cada átomo es considerado como un cuerpo de masa m, la Fi
ecuación que determina la aceleración a a la que éste es sometido debido la existencia de fuerzas entre éste y
el resto de átomos de la propia proteína o del solvente, es la siguiente:
N
I
Fi = m · a (1)
i=1
Siendo N el número de átomos. La aceleración a a la que está sometido un cuerpo es la derivada respecto del tiempo de la velocidad v
del mismo. .
Por tanto dicha velocidad puede ser obtenida de la integración respecto del tiempo de la mencionada aceleración a
De igual modo la posición x es obtenida como la integral respecto del tiempo de la velocidad v dado que ésta es la derivada de aquélla. De este modo la posición de cada átomo puede ser obtenida mediante integración a partir de la velocidad y ésta a su vez mediante integración de la aceleración que, conocidas las fuerzas que actúan sobre dicho átomo, nos proporciona la anterior ecuación 1.
De igual manera para similar las condiciones reales de las proteínas, y en general de las biomoléculas, se rodea a la molécula de un solvente, agua, simulando las condiciones de la célula. Este solvente es necesario para ciertos procesos biológicos, como el plegamiento de proteínas dónde el carácter hidrófilo o hidrofóbico es clave para determinar su estructura.
Esto requiere simular además de la proteína a estudio, miles de moléculas de agua que simulan el solvente, por lo que los sistemas a estudio cuentan con miles de átomos a simular.
Por motivos similares, para simular las condiciones experimentales de los sistemas macroscópicos, se introducen las llamadas condiciones periódicas de frontera (véase T. Schlick, Molecular Modeling and Simulation: An Interdisciplinar y Guide. Interdisciplinar y Applied Mathematics series, vol. 21. Springer: New York, pp272–6. 2002) . De esta manera el sistema (biomoléculas más solvente) que queremos simular se rodea de copias periódicas de sí mismo en las 3 direcciones. Esta es una manera computacionalmente abordable de simular las condiciones de los sistemas, dónde se tienen un elevado número de moléculas (del orden del número de Avogadro) .
Una manera eficiente de calcular la fuerza que actúa sobre un átomo debido a su interacción con estas copias, es el llamado Particle Mesh Ewald (T. Darden, D. M.York, L. G. Pedersen , Particle mesh Ewald: An N log (N) method for Ewald sums in large Systems, J. Chem. Phys. (Communication) 98, 10089-10092 (1993) ) . Antes de entrar en detalle sobre los diferentes tipos de fuerza y la problemática que plantean, es conveniente hablar de la base de la Dinámica Molecular, la resolución de la segunda ley de Newton, ecuación 1. Se trata de una ecuación diferencial de segundo orden en la posición y por tanto su resolución pasa por una integración.
Esta ecuación es equivalente a un sistema de ecuaciones de primer orden, las denominadas ecuaciones de Hamilton, en lo que se llama formalismo hamiltoniano (véase B. Leimkuhler, S. Reich, Simulating Hamiltonian dynamics, Cambridge University Press 2004) .Dado que estas soluciones no son resolubles analíticamente en casos como la Dinámica Molecular, es necesaria una resolución numérica de dichas ecuaciones diferenciales.
Dicha resolución, llamada integración numérica, se basa en el paso de un tiempo continuo a uno discreto. La separación entre cada uno de los instantes de tiempo discreto se le denomina paso de tiempo o timestep. Partiendo de unas condiciones iniciales de posición y velocidad, se trata de hallar sus valores en todos los instantes posteriores. A la función que, a partir del valor de posición y velocidad en un instante, permite obtener un valor para el instante siguiente, se le denomina integrador. Por tanto, el integrador y el paso de tiempo son los que determinan la calidad de la simulación.
Dado que al pasar de un tiempo continuo a uno discreto estamos realizando una aproximación, cuando mayor es el paso de tiempo, peor es la resolución de la ecuación diferencial.
Puede ocurrir que si elegimos un paso de tiempo demasiado grande la solución que obtenemos no tenga nada que ver con la real y diverja. En ese caso se dice que para ese paso de tiempo el integrador es inestable. El rango de valores de paso de tiempo para los que un integrador es estable se denomina zona de estabilidad (véase E. Hairer,
S. P. Nørsett, Gerhard Wanner, Solving ordinar y differential equations I: Nonstiff problems, second edition, Springer
Verlag, Berlin, 1993) Las fuerzas Fi a las que cada átomo está sometido son de distinta naturaleza en cuanto a su magnitud, su variabilidad en el tiempo y son función de la posición de los restantes átomos de la proteína o de los átomos del solvente.
El proceso de integración numérica anteriormente comentado está basado en ir avanzando la simulación a intervalos de tiempo hasta alcanzar el tiempo final de la misma. Debido a la altísima frecuencia (variabilidad en el tiempo) de algunas de las fuerzas Fi estos intervalos de tiempo son pequeñísimos, del orden de los femtosegundos (10-15
segundos) . Los tiempos totales de simulación requeridos para por ejemplo simular el plegamiento completo de una proteína van desde los microsegundos hasta varios minutos (David Sheehan, Physical Biochemistr y , Second Edition, John Wiley & Sons, 2009) por tanto el...
Reivindicaciones:
1. Método implementado por ordenador para simular sistemas de átomos mediante dinámica molecular, que comprende el empleo de al menos un integrador numérico para integrar las ecuaciones de movimiento de los átomos de dicho sistema, caracterizado porque además comprende controlar la potencia de al menos parte de los átomos del sistema a simular, modificando adaptativamente el valor del paso de tiempo de dicho integrador numérico, manteniendo la potencia dentro de un rango de estabilidad de potencia dentro del cual se considera que la simulación del sistema es estable, y mediante dicho ordenador integrar las ecuaciones de movimiento de los átomos al ritmo marcado por el paso de tiempo elegido para el integrador.
2. Método según la reivindicación 1 caracterizado porque se lleva a cabo un bucle de control de potencia en el que se calcula la potencia de al menos parte de los átomos del sistema a simular, y se modifica adaptativamente el paso de tiempo de dicho integrador numérico en función de la potencia de los átomos calculada, de modo que si la potencia es menor que un umbral inferior del rango de estabilidad se aumenta el paso de tiempo del integrador, y de modo que si la potencia es mayor que un umbral superior del rango de estabilidad se reduce el paso de tiempo del integrador, y mediante dicho ordenador integrar las ecuaciones de movimiento de los átomos en los tiempos marcados por el paso de tiempo elegido en cada instante para el integrador.
3. Método según la reivindicación 1 o 2 caracterizado porque además comprende reducir la velocidad de los átomos cuya potencia supere un umbral superior del rango de estabilidad, con objeto de mantener la estabilidad de la simulación.
4. Método según la reivindicación 3 caracterizado porque la reducción de la velocidad de los átomos se realiza mediante el escalado de la velocidad del átomo, de modo que la nueva potencia del átomo se iguala a la del umbral superior del rango.
5. Método según cualquiera de las reivindicaciones anteriores caracterizado porque el umbral superior se define como cien veces el valor máximo de las variables dinámicas del sistema, para una simulación a paso de tiempo constante de 0.5 femtosegundos, y un umbral inferior se define como cien veces el valor mínimo de estas variables dinámicas para la misma simulación.
6. Método según cualquiera de las reivindicaciones anteriores caracterizado porque la potencia de los átomos se calcula como el producto escalar de la velocidad del átomo por la fuerza que actúa sobre él.
7. Método según cualquiera de las reivindicaciones anteriores caracterizado porque comprende el empleo de un integrador numérico que incluye algoritmos de ligaduras, seleccionados entre: Shake, Rattle, or Wiggle, que se aplican a variables que representan a las fuerzas y velocidades de los átomos del sistema, y donde dichos algoritmos de ligaduras se emplean para la imposición de restricciones a las componentes de alta frecuencia de las fuerzas de enlace del sistema de átomos, y la repartición de la masa de los átomos de hidrógeno.
8. Método según cualquiera de las reivindicaciones anteriores caracterizado porque se definen dos o más rangos de estabilidad, cada uno asociado a un átomo distinto del sistema.
9. Método según cualquiera de las reivindicaciones anteriores caracterizado porque la integración de las ecuaciones de movimiento de los átomos consiste en una integración con múltiples pasos de tiempo (MTS) , y se controla de manera independiente los diferentes pasos de tiempos en base a la potencia calculada con las fuerzas y velocidades para cada paso de la integración.
10. Método según cualquiera de las reivindicaciones anteriores caracterizado porque el sistema de átomos a simular se corresponde con: un gas, un líquido, un nano-dispositivo, biomoléculas, o proteínas.
11. Método según cualquiera de las reivindicaciones anteriores caracterizado porque el método está adaptado para la selección de fármacos, y porque el sistema de átomos a simular se corresponde con una biomolécula, y porque el método comprende introducir en dicho ordenador datos correspondientes al fármaco a simular, y una vez completada la simulación, generar datos referentes a la dinámica de las moléculas que comprenden: posiciones, velocidades, y energías.
12. Sistema para simular sistemas de átomos mediante dinámica molecular, que comprende al menos un ordenador programado para integrar las ecuaciones de movimiento de los átomos del sistema mediante al menos un integrador numérico, caracterizado porque además dicho al menos un ordenador está programado para controlar la potencia de al menos parte de los átomos del sistema a simular, modificando adaptativamente el valor del paso de tiempo de dicho integrador numérico.
13. Sistema según la reivindicación 12 caracterizado porque el ordenador comprende medios de entrada de datos, medios de salida de datos, un procesador y un programa de ordenador almacenado en la memoria del ordenador, donde dicho programa está adaptado para la selección de fármacos, y porque el sistema de átomos a simular se corresponde con una biomolécula, y porque dicho programa al ser ejecutado por dicho procesador, está adaptado a generar datos referentes a la dinámica de las moléculas que comprenden: posiciones, velocidades, y energías.
14. Sistema según la reivindicación 12 o 13 caracterizado porque el programa se lleva a cabo un bucle de control de potencia en el que se calcula la potencia de al menos parte de los átomos del sistema a simular, y se modifica adaptativamente el paso de tiempo de dicho integrador numérico en función de la potencia de los átomos calculada,
de modo que si la potencia es menor que un umbral inferior del rango de estabilidad se aumenta el paso de tiempo del integrador, y de modo que si la potencia es mayor que un umbral superior del rango de estabilidad se reduce el paso de tiempo del integrador, y mediante dicho ordenador integrar las ecuaciones de movimiento de los átomos en los tiempos marcados por el paso de tiempo elegido en cada instante para el integrador.
15. Programa de ordenador adaptado para el estudio de fármacos, configurado de forma que cuando se ejecuta en un ordenador es capaz de implementar el método definido en cualquiera de las reivindicaciones 1 a 11.
Patentes similares o relacionadas:
MÉTODO IMPLEMENTADO POR ORDENADOR, SISTEMA Y PRODUCTO DE PROGRAMA PARA ORDENADOR PARA SIMULAR EL COMPORTAMIENTO DE TEXTIL TEJIDO A NIVEL DE HILO, del 19 de Enero de 2017, de UNIVERSIDAD REY JUAN: Método implementado por ordenador, sistema y producto de programa de ordenador para simular el comportamiento de un textil tejido a nivel de hilo. El método comprende: - recuperar […]
Método implementado por ordenador, sistema y producto de programa para ordenador para simular el comportamiento de textil tejido a nivel de hilo, del 16 de Enero de 2017, de UNIVERSIDAD REY JUAN CARLOS: Método implementado por ordenador, sistema y producto de programa de ordenador para simular el comportamiento de un textil tejido a nivel de hilo. El […]
METODO PARA MODELADO DE OBJETOS TRIDIMENSIONALES Y PARA SIMULACION DE FLUJO DE FLUIDOS., del 1 de Diciembre de 2005, de MOLDFLOW PTY. LTD.: Un procedimiento para simular flujo de fluido dentro de un objeto tridimensional que consta de una primera y de una segunda superficie generalmente […]