MÉTODO PARA LA GENERACIÓN DE MODELOS REALISTAS EN TRES DIMENSIONES DE CÉLULAS NEURONALES.
Esta invención presenta un método para la generación de modelos tridimensionales de células neuronales partiendo de la información morfológica incompleta extraída mediante métodos de muestreo estándar.
Los modelos generados incluyen un soma realista, árboles dendríticos y axonales, y espinas dendríticas, pudiendo ser generados a diferentes niveles de resolución. La invención propone una técnica innovadora que permite obtener una forma realista del soma partiendo de una definición simple del mismo (tal como centro y radio) que resulta incompleta para reconstruir la forma 3D original. El método propuesto se basa en la deformación de una forma inicial, guiada por restricciones establecidas de acuerdo a las propiedades morfológicas de los árboles dendríticos y axonales (por ejemplo: posición y grosor de las dendritas de primer orden). La distribución de un conjunto de espinas a lo largo de las dendritas completa el modelo, generando un modelo tridimensional adecuado para su visualización en una amplia gama de entornos 3D.
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P201330231.
Solicitante: UNIVERSIDAD REY JUAN CARLOS.
Nacionalidad solicitante: España.
Inventor/es: BAYONA BERISO,SOFIA, MATA FERNANDEZ,Susana, BRITO MENENDEZ,Juan Pedro, PASTOR PEREZ,Luis, BENAVIDES PICCIONE,Ruth, DE FELIPE OROQUIETA,Javier.
Fecha de Publicación: .
Clasificación Internacional de Patentes:
- G06T17/20 FISICA. › G06 CALCULO; CONTEO. › G06T TRATAMIENTO O GENERACIÓN DE DATOS DE IMAGEN, EN GENERAL. › G06T 17/00 modelado 3D mediante gráficos de computdor. › Descripción marco de alambre, p. ej. formando polígonos o teselas.
Fragmento de la descripción:
Campo de la invención
La presente invención se encuadra dentro del campo de la reconstrucción de las células neuronales. Más específicamente se refiere a la generación de mallas poligonales 3D que aproximan la forma del soma y la de los árboles dendríticos y axonales, utilizando como punto de partida datos morfológicos incompletos obtenidos de la célula.
Estado de la técnica
Se han realizado importantes contribuciones en el campo de la utilización de enfoques de visualización para sistemas complejos, aplicándose con éxito para el diseño y el análisis de una variedad de sistemas complejos, utilizando la capacidad del sistema visual humano para extraer información de escenarios visuales. En particular, la visualización analítica o la visualización de datos son campos de investigación activos y extremadamente multidisciplinares cuyo objetivo es proporcionar representaciones gráficas de los datos para mejorar la comprensión del fenómeno observado. De hecho, los beneficios de la incorporación de enfoques basados en la visualización para el análisis de sistemas complejos ya son evidentes en la investigación neurocientífica. Por ejemplo, recientemente se ha desarrollado un método basado en la aplicación de transformaciones de enderezamiento y desenrollamiento para transformar la estructura original de las inserciones de las espinas en las dendritas de células piramidales a una disposición desenrollada plana (Morales, J., Benavides-Piccione, R., Rodriguez, A., Pastor, L., Yuste, R., & Defelipe, J. (2012). "Three-dimensional analysis of spiny dendrites using straightening and unrolling transforms. Neuroinformatics, doi: 10.1007/s12021-012-9153-2)., permitiendo una nueva forma de comprender la organización y los patrones de distribución de estas células.
La reconstrucción de células neuronales ha evolucionado desde las imágenes dibujadas a mano (basadas en las técnicas tradicionales de imagen microscópica con cámara lúcida) a las actuales morfologías tridimensionales digitalizadas extraídas mediante aplicaciones de trazado asistido por ordenador. Estas reconstrucciones se
han utilizado para medir los parámetros geométricos de árboles neuronales reales y simular morfologías de neuronas virtuales (López, PL, Bielza C, Larrañaga P, Benavides-Piccione R, DeFelipe J (2011) Models and simulation of 3D neuronal dendritic trees using Bayesian networks. Neuroinformatics 9:347-369). La información morfológica extraída con estas aplicaciones típicamente está compuesta de un determinado número de puntos conectados entre sí que trazan el esqueleto de la neurona, capturando la forma y las trayectorias tanto de las dendritas como del axón en tres dimensiones, lo que permite el estudio de diversos parámetros morfológicos como las características de las dendritas/axón y el soma. No obstante, en el caso concreto de la forma del soma (el cuerpo de la neurona), la información de partida consiste a menudo en un grupo de puntos que delimitan su contorno en 2D. Estudios previos no consideran la forma del soma o, en el mejor de los casos, representan el soma con una esfera, lo que no necesariamente coincide con la morfología real. En la actualidad, la única alternativa para obtener una representación más precisa de la forma real del soma es su reconstrucción a partir de las imágenes seriadas de microscopia confocal. Para poder reconstruir la morfología real, este conjunto de imágenes deben ser procesados con determinados softwares muy costosos no disponibles en la gran mayoría de los laboratorios..
Además, en la actualidad no hay ningún método disponible para la reconstrucción de la forma del soma que proporcione una representación 3D del mismo cuando la información de partida es incompleta. Esta es la manera mas generalizada de reconstrucción de neuronas actualmente en la comunidad científica. Dicha información incompleta sobre el soma, a menudo consiste, como mencionábamos anteriormente, en puntos del contorno 2D del soma, o incluso la definición de un punto central (representando el centro del soma) y un radio. En la actualidad no hay información suficiente para reconstruir la forma original en 3D a partir de estos archivos.
La presente invención simula la deformación que se produciría sobre una forma inicial, en nuestro caso una esfera, si las dendritas que parten del soma tiraran de ella. Dicha deformación se propaga, hasta que el soma alcanza su forma final, utilizando una técnica de deformación como la de masa-muelle. La simulación es abordada como un problema de minimización de energía, ya que una superficie asumirá una deformación que minimice la energía total de deformación (Terzopoulos et al. 1987). La técnica
aquí descrita puede también ser utilizada por los laboratorios que definen el soma proporcionando únicamente el centro y su radio.
Problema técnico a resolver
La presente invención resuelve el problema técnico de generar una representación tridimensional de la forma de una célula, a partir de los datos incompletos de su morfología, extraídos mediante aplicaciones de trazado comúnmente utilizadas en la comunidad científica. Para ello se aplica una nueva técnica que aproxima la forma de la célula a través de mallas poligonales 3D, a partir de dicha información morfológica incompleta. En particular, la presente técnica utiliza el sistema de deformación masa- muelle ya que es uno de los modelos de deformación más sencillos. De forma complementaria también genera mallas de alta calidad de los árboles dendríticos y axonales, incluyendo también reconstrucciones detalladas de las espinas dendríticas Esta técnica crea y conecta los elementos de forma suave, para una mejor visualización, y permite la aplicación de algoritmos gráficos tanto estándar como avanzados de mapeo de estructuras, sombreado o procesamiento de geometría. Además, la invención permite la obtención de mallas 3D a diferentes niveles de resolución, posibilitando así el tener modelos apropiados para técnicas de visualización con multirresolución.
Una ventaja adicional de este método es la posibilidad de reconstruir los modelos 3D de todas las células neuronales almacenadas en diferentes bases de datos actuales, que contienen información incompleta de la forma tridimensional del soma, para obtener una representación mucho más realista.
Descripción de la invención
Esta invención presenta un método para generar modelos de células neuronales en tres dimensiones a partir de la información morfológica extraída por métodos de muestreo. Típicamente este muestreo proporciona un conjunto de puntos 3D conectados (con sus posiciones y radios asociados) que representan el esqueleto de la neurona. Este esqueleto puede ser procesado posteriormente para obtener características relevantes de su morfología, tales como la longitud de las dendritas, el número de bifurcaciones, número de terminaciones, etc. La malla poligonal en 3D que aproxima la membrana celular se puede generar con diferentes grados de resolución, manteniendo un compromiso entre la complejidad y la calidad final del modelo. La
principal contribución de la presente invención es proponer una aproximación novedosa para generar modelos en 3D del soma con una morfología realista a partir de los datos incompletos de la estructura morfológica descrita anteriormente. Esta técnica se basa en la deformación, de una forma inicial, en función de características de los árboles dendríticos/axonal, como por ejemplo la posición y el grosor de las dendritas de primer orden (las dendritas que parten directamente del soma). El modelo se completa con la generación de árboles axonales y dendríticos continuos y la inclusión opcional de las espinas en las dendritas, generando así un modelo neuronal 3D completo que permite su visualización en un amplio rango de entornos 3D.
El método para la generación de modelos neuronales realistas en 3D a partir de los datos morfológicos incompletos de la célula comprende 3 etapas:
1.- Construcción del soma: esta etapa obtiene una forma 3D muy aproximada a la forma real del soma, partiendo de una descripción incompleta: el contorno 2D del soma (3A) o la posición del centro y el radio del soma. Esta etapa conlleva los siguientes pasos:
1.a.- Construir una forma inicial simple a partir de los datos incompletos.
Esta forma simple puede obtenerse de diferentes maneras; una opción es generar una esfera que contenga completamente el soma (3B) y reducirla de acuerdo con un parámetro establecido (3C). En una realización preferente, esta reducción puede estar comprendida entre un 10% y un 30%. La esfera es representada como una malla poligonal.
1.b.- Seleccionar el mecanismo de deformación...
Reivindicaciones:
1.- Método para la generación de modelos realistas en tres dimensiones de células neuronales a partir de los trazados morfológicos extraídos en los laboratorios de neurociencia que comprende:
- obtener una definición morfológica de la neurona (1) que contenga al menos una pluralidad de puntos morfológicos (5);
- generar un modelo en tres dimensiones de los árboles dendríticos y axonales;
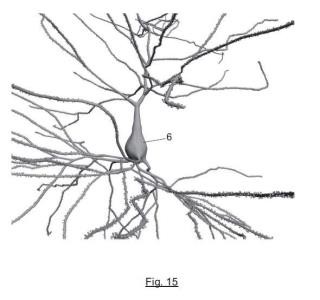
- generar un modelo tridimensional del soma (6) mediante:
la generación de una forma inicial tridimensional del soma (6) a partir de la definición morfológica;
la aplicación de un modelo de deformación mecánica a la forma inicial tridimensional del soma, considerando un conjunto de restricciones extraídas de las propiedades morfológicas de las dendritas y axón para obtener una forma deformada (14) del soma (6);
- unir dichos modelos tridimensionales generados en un único modelo tridimensional de la neurona (1).
2.- Método de acuerdo con la reivindicación 1, caracterizado porque las restricciones incluyen al menos la posición y el grosor de los segmentos iniciales (7) de las dendritas de primer orden (3).
3.- Método de acuerdo con la reivindicación 2, caracterizado porque la generación del modelo tridimensional del soma (6) comprende la obtención, a partir de la definición morfológica del soma (6), de una esfera envolvente (10) del soma (6), y donde la forma inicial tridimensional del soma (6) es una esfera reducida (11) obtenida como una reducción de la esfera envolvente (10) de acuerdo a un parámetro de reducción.
4.- Método de acuerdo con la reivindicación 3, caracterizado porque el parámetro de reducción está comprendido en un rango entre el 10% y 30%.
5.- Método de acuerdo con cualquiera de las reivindicaciones 3 ó 4, caracterizado porque la generación del modelo tridimensional del soma (6) comprende las siguientes etapas:
- representar la esfera reducida (11) como una malla poligonal tridimensional;
- definir, en dicha malla poligonal tridimensional, la región de influencia (12) de cada dendrita de primer orden (3);
- calcular el desplazamiento de los vértices (13, 13) de la malla poligonal tridimensional bajo dicha región de influencia (12) de acuerdo al conjunto de restricciones previamente definidas;
- calcular las fuerzas a aplicar en los vértices (13, 13) de cada región de influencia (12) que satisfagan dichas restricciones de desplazamiento;
- obtener una forma deformada (14) del soma (6) mediante la propagación de dichas fuerzas sobre la malla poligonal tridimensional, utilizando un modelo de deformación mecánica.
6.- Método de acuerdo con la reivindicación 5, caracterizado porque adicionalmente comprende la obtención, a partir de la forma deformada (14), de una malla del soma deformado (15) mediante:
- el desplazamiento de los vértices (13) del contorno de cada región de influencia (12) de forma que el diámetro de la región de influencia (12) coincida con el grosor inicial de la correspondiente dendrita de primer orden (3);
- la aplicación de una triangulación en forma de abanico entre los vértices (13) del contorno y el vértice central (13) y la eliminación del resto de los vértices y triángulos de la superficie de la región de influencia (12).
7.- Método de acuerdo con cualquiera de las reivindicaciones 5 o 6, caracterizado porque el modelo de deformación mecánica es un modelo masa-muelle.
8.- Método de acuerdo a la reivindicación 7, caracterizado porque el modelo masa- muelle se genera en la malla poligonal tridimensional, mediante la creación de una estructura de muelles en las aristas de los triángulos de la esfera reducida (11) y un conjunto de muelles internos que parten del centro de la malla.
9.- Método de acuerdo con cualquiera de las reivindicaciones 7 a 8, caracterizado porque la esfera reducida (11) se modela como una serie de masas puntuales conectadas por muelles siguiendo la Ley de Hooke, aplicando posteriormente la Segunda Ley de Newton a las masas puntuales, incluyendo las fuerzas aplicadas por los muelles.
10.- Método de acuerdo a cualquiera de las reivindicaciones de la 5 a la 9, caracterizado porque la región de influencia (12) de cada dendrita de primer orden (3) se determina de acuerdo con el grosor de la misma.
11.- Método de acuerdo con cualquiera de las reivindicaciones 5 a 10, caracterizado porque el desplazamiento de la región de influencia (12) asociada a una dendrita de primer orden (3) se determina de acuerdo a la posición inicial de dicha dendrita.
12.- Método de acuerdo con cualquiera de las reivindicaciones anteriores, caracterizado porque la generación del modelo tridimensional de los árboles dentríticos y axonales comprende la representación de cada segmento (17) del esqueleto morfológico definido por los puntos morfológicos (5) como un tronco de cono (18), en el que los radios de las bases (19) son los radios definidos por los puntos morfológicos (5) en los extremos del segmento (17).
13.- Método según la reivindicación 12, caracterizado porque adicionalmente comprende la unión del soma deformado (15) con los conos truncados (18) de las dendritas de primer orden (3), mediante la eliminación, en cada correspondiente región de influencia (12), de los triángulos que conectan con el vértice central (13') y el desplazamiento de los vértices (13'') del contorno de la región de influencia (12) de manera que queden coincidentes con los vértices del segmento inicial (7) de la correspondiente dendrita de primer orden.
14.- Método de acuerdo con cualquiera de las reivindicaciones 12 a 13, caracterizado porque la resolución de cada tronco de cono (18) está dada por al menos dos parámetros ajustables:
- el número de secciones transversales (20) entre las dos bases (19); y
- el número de puntos (21) utilizados para aproximar la forma circular de las bases (19).
15.- Método según cualquiera de las reivindicaciones 12 a 14, caracterizado porque adicionalmente comprende la unión de los conos truncados consecutivos (18a, 18b), mediante la triangulación de los puntos que definen la última sección transversal del primer cono truncado (18a) con los puntos que definen la primera sección del segundo
cono (18b), y por el acortamiento del primer cono (18a) y la reorientación de la base adyacente (19) del segundo cono truncado (18b).
16.- Método según la reivindicación 15, caracterizado porque adicionalmente comprende la unión de los conos truncados (18a, 18b, 18c) en los puntos de bifurcación (24) primero uniendo dos conos truncados consecutivos (18a, 18b) y luego conectando los dos conos truncados ya unidos (18a , 18b) con el tercer cono truncado (18c), mediante la apertura de un orificio (23) en la malla de los dos conos truncados unidos (18a, 18b) y la unión de la primera sección del tercer cono truncado (18c) a los vértices del contorno del agujero (23).
17.- Método de acuerdo con cualquiera de las reivindicaciones anteriores, caracterizado porque comprende además la generación de modelos tridimensionales de las espinas dendríticas (4).
18.- Método según la reivindicación 17, caracterizado porque las espinas (4) se generan como una serie de anillos concéntricos cuyos radios aumentan progresivamente desde la base hasta la parte superior de la espina (4).
19.- Método según la reivindicación 18, caracterizado porque comprende además la distribución de los modelos tridimensionales generados de las espinas (4) a lo largo del modelo tridimensional de la neurona (1).
20.- Método según la reivindicación 19, caracterizado porque la distribución de las espinas (4) se realiza siguiendo una función de distribución.
Patentes similares o relacionadas:
Sombreado de representaciones CG de materiales, del 18 de Marzo de 2020, de Chaos Software Ltd: Un aparato para escanear muestras de material, el aparato comprendiendo: una fuente de luz colimada que tiene una lente para emitir luz colimada; un segundo […]
Un procedimiento y disposición para proporcionar un modelo 3d, del 8 de Enero de 2020, de Vricon Systems Aktiebolag: Un procedimiento para proporcionar un modelo 3D de un entorno que comprende el paso de formar una red que modela el entorno […]
Malla adaptativa de resolución para realizar metrología en 3-d de un objeto, del 6 de Noviembre de 2019, de THE BOEING COMPANY: Un metodo (200, 200') para generar una malla adaptativa de resolucion para la metrologia 3-D de un objeto , que comprende: recibir […]
Metrología en vivo de un objeto durante la fabricación u otras operaciones, del 21 de Agosto de 2019, de THE BOEING COMPANY: Un método para metrología en vivo de un objeto, que comprende: realizar una operación de escaneado mediante una pluralidad de sensores para […]
 Voxelización de una malla, del 29 de Mayo de 2019, de Biosense Webster (Israel), Ltd: Un procedimiento para la representación tridimensional (3D), que comprende:
recibir un grupo de triángulos 3D que definen una malla triangular […]
Voxelización de una malla, del 29 de Mayo de 2019, de Biosense Webster (Israel), Ltd: Un procedimiento para la representación tridimensional (3D), que comprende:
recibir un grupo de triángulos 3D que definen una malla triangular […]
Método de fabricación y ensamblaje y sistema de partes de una aeronave, del 24 de Mayo de 2019, de Airbus Defence and Space SAU: Método de fabricación y ensamblaje de partes de una aeronave que comprende los pasos siguientes: a) proporcionar una primera parte de aeronave […]
Método para evaluar el impacto de fracturas pre-existentes y fallas en la gestión de reservorios, del 20 de Diciembre de 2017, de REPSOL S.A: Método implementado por ordenador para evaluar el impacto de fallas y fracturas existentes para la gestión de reservorios, comprendiendo: generar un […]
Sistema interactivo de acceso a la información, del 18 de Enero de 2016, de PEA ORCASITA, Julio César: Sistema interactivo de acceso a la información. Sistema que comprende al menos una unidad de control y al menos una pantalla táctil que puede ser una pantalla LCD, […]