METODO DE MANTENIMIENTO PREDICTIVO DE BATERIAS.
Método de mantenimiento predictivo de baterías, especialmente de baterías cuya vida media sea relativamente larga y que se encuentren instaladas en entornos cuya temperatura no esté controlada,
de forma que se pueda determinar con garantías el tiempo de vida útil remanente de las mismas basado en, una vez establecidos los criterios de aceptación y rechazo de una batería, conocer cuánto tiempo tardará en llegar a los valores críticos de funcionamiento partiendo de un estado conocido para así poder establecer un plan de mantenimiento predictivo que garantice que la vida útil (L) de la batería es mayor que el periodo de inspección establecido
Tipo: Patente de Invención. Resumen de patente/invención. Número de Solicitud: P200930322.
Solicitante: METRO DE MADRID, S.A..
Nacionalidad solicitante: España.
Provincia: MADRID.
Inventor/es: SANCHO DE MINGO,CARLOS, GARCIA SAN ANDRES,MARIA ANTONIA, GONZALEZ FERNANDEZ,FRANCISCO J, MUÑOZ CONDES,PILAR, GOMEZ PARRA,MIGUEL.
Fecha de Solicitud: 17 de Junio de 2009.
Fecha de Publicación: .
Fecha de Concesión: 20 de Mayo de 2011.
Clasificación Internacional de Patentes:
- G01R31/36V3
- G01R31/36V6
Clasificación PCT:
- G01R31/36 FISICA. › G01 METROLOGIA; ENSAYOS. › G01R MEDIDA DE VARIABLES ELECTRICAS; MEDIDA DE VARIABLES MAGNETICAS (indicación de la sintonización de circuitos resonantes H03J 3/12). › G01R 31/00 Dispositivos para ensayo de propiedades eléctricas; Dispositivos para la localización de fallos eléctricos; Disposiciones para el ensayo eléctrico caracterizadas por lo que se está ensayando, no previstos en otro lugar (ensayo o medida de dispositivos semiconductores o de estado sólido, durante la fabricación H01L 21/66; ensayo de los sistemas de transmisión por líneas H04B 3/46). › Dispositivos para el ensayo, medida o monitorización del estado eléctrico de acumuladores o baterías, p. ej. de la capacidad o del estado de la carga [SoC].
Fragmento de la descripción:
Método de mantenimiento predictivo de baterías.
Objeto de la invención
La presente solicitud de Patente de Invención tiene por objeto, como su propio nombre indica, el establecimiento de un método de mantenimiento predictivo de baterías, especialmente de baterías cuya vida media sea relativamente larga y que se encuentren instaladas en entornos cuya temperatura no esté controlada, de forma que se pueda determinar con garantías el tiempo de vida útil remanente de las mismas.
Más concretamente, el método de la presente invención se basa en, una vez establecidos los criterios de aceptación y rechazo de una batería, conocer cuánto tiempo tardará en llegar a los valores críticos de funcionamiento partiendo de un estado conocido para así poder establecer un plan de mantenimiento predictivo.
Antecedentes de la invención
Actualmente, el uso de baterías está ampliamente extendido, utilizándose éstas en innumerables aplicaciones y sectores de la técnica en donde es necesario asegurar la operación de equipos eléctricos críticos tanto en entornos estáticos controlados, como por ejemplo instalaciones industriales de generación eléctrica, sistemas telefónicos, servicios de emergencia, respaldo de sistemas informáticos, etc., como en entornos dinámicos en donde las condiciones de trabajo y la problemática asociada a dichas condiciones difieren sustancialmente de una aplicación estacionaria, como sucede por ejemplo en el entorno ferroviario, en donde las baterías se utilizan para aportar la energía de servicio mínima necesaria ante un fallo en el funcionamiento de los equipos de alimentación principales.
Aunque son conocidos en el estado de la técnica métodos para realizar el diagnóstico puntual de las baterías a partir de un parámetro crítico, como por ejemplo la impedancia, no se conocen metodologías de mantenimiento predictivo capaces de prever la evolución en el tiempo de dicho parámetro crítico. Dicho de otra forma, no se conocen procedimientos de mantenimiento predictivo capaces de estimar qué valor de aceptación - rechazo de la batería debe fijarse para asegurar que dentro de un periodo fijo de tiempo la batería no va estar funcionando en una determinada zona crítica, especialmente para los casos en los que dichas baterías cuentan con una vida media relativamente larga, de 5 o más años, y que se encuentren instaladas en entornos cuya temperatura no esté controlada.
Por ejemplo, dado que la vida media estimada por los fabricantes de baterías de tracción ferroviarias es de al menos 10 años, para realizar un estudio completo de mantenimiento predictivo sería deseable utilizar al menos la información durante todos esos años. Esto serviría para conocer en detalle la evolución de los valores del parámetro crítico (impedancia de módulo, impedancia de vaso u otros) de un parque de baterías.
Sin embargo, en la práctica generalmente no se dispone de plazos tan amplios para estudios de sistemas como el planteado, por lo que se hace necesaria la toma de muestras en un periodo de tiempo mucho más corto para su posterior extrapolación en el tiempo.
Esto presenta un serio inconveniente, pues los parámetros factibles de ser escogidos como representativos del estado de las baterías suelen tener un comportamiento errático si se consideran en el corto plazo. Sin embargo, el estudio de esos mismos parámetros en plazos de tiempo del orden de la vida útil prevista de la batería presenta tendencias claramente definidas.
El comportamiento pseudo-aleatorio de la impedancia en el corto plazo hace que cualquier extrapolación realizada a partir de datos tomados en intervalos de tiempo reducidos lleve asociada un error que puede ser importante, siendo a todas luces inadmisible para la implantación de un sistema de mantenimiento predictivo.
En otras palabras, la extrapolación del valor de Z en el tiempo sería una función con un coeficiente de correlación R2 muy bajo, lo que impide tratar el problema de una forma determinista, consistente en encontrar la función de impedancia frente al tiempo (Z = f(t)).
Descripción de la invención
El método para el mantenimiento predictivo de baterías de la invención que a continuación se describe resuelve los inconvenientes antes señalados, pues proporciona un sistema eficaz y fiable para el diagnóstico en el tiempo del estado de baterías cuya vida media sea relativamente larga y que se encuentren instaladas en entornos cuya temperatura no esté controlada, es decir, un método capaz de asegurar que una batería dada por buena aguante en óptimas condiciones hasta la próxima revisión.
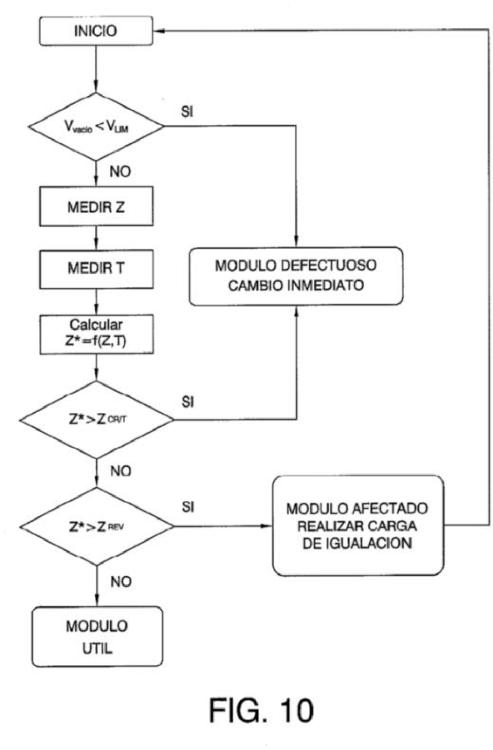
De forma general, el método de mantenimiento predictivo de baterías de la presente invención se basa en los siguientes pasos:
1º. Definir, para un periodo de revisión determinado, los valores de aceptación/rechazo para saber si el elemento revisado debe ser intervenido o no.
2º. Establecer una tendencia para elemento revisado, que permita establecer el periodo de tiempo máximo previsto para realizar la siguiente revisión antes de que se alcance el valor de rechazo.
3º. Finalmente, para cada aplicación de la batería se determinarán a partir de la información obtenida de los dos primeros los plazos de mantenimiento óptimos.
Para el caso de la presente invención, dichos valores de aceptación/rechazo se basan en los valores de impedancia, que podría ser tanto de vaso como de módulo, por lo que el parámetro crítico o la variable de diagnosis será dicha impedancia.
Como ya se explicó en el apartado anterior, no se puede tratar el problema de una forma determinista, pues no se puede encontrar ninguna función de impedancia de módulo frente al tiempo (Z = f(t)) con un ajuste lo suficientemente bueno.
Para evitar ese importante inconveniente en la presente invención se plantea un método de mantenimiento predictivo basado en la evaluación de la variación de la impedancia en el tiempo.
Sin embargo, tampoco es posible hallar una función determinista de la evolución de la variación de impedancia, ya que dichas variaciones de impedancia en el tiempo pasan por las mismas dificultades que los valores discretos de la impedancia. Es decir, si se trabaja con periodos muy cortos en comparación con la vida media de las baterías, se introducen variaciones muy acusadas en los valores de las variaciones de impedancia.
Esto obliga a realizar un cambio de planteamiento que posibilite la obtención de un método de mantenimiento predictivo fiable.
Dicho cambio de planteamiento se basa en el hecho de que para la implantación de un método de mantenimiento predictivo no se necesita conocer con exactitud la vida útil (L) remanente de la batería en cualquier instante de tiempo, sino que es suficiente con garantizar que dicha vida útil (L) es mayor que el periodo de inspección establecido.
Así, utilizando la impedancia como parámetro crítico y sabiendo que la impedancia tiende a ser creciente en el tiempo, se podrá fijar un valor crítico (Zcrit) por debajo del cual se pueda garantizar un funcionamiento óptimo de la batería.
Se define ΔZ(t) como la variación de impedancia que experimenta una batería en el plazo de t meses.
Se define ΔZmax(t) como el valor supremo de todos los posibles valores de ΔZ(t); es decir:
De acuerdo a las definiciones anteriores, una batería con impedancia Z permanecerá durante un tiempo t en buenas condiciones de funcionamiento siempre y cuando se verifique:
El problema se reduce a calcular la variable ΔZmax(t).
Dado que no se puede demostrar que ΔZ(t) esté acotada superiormente, se supondrá con carácter general que no existe dicha acotación. Esto implica que no existe el valor supremo, y por tanto ΔZmax(t) quedaría indefinida.
Sin embargo se puede utilizar una muy buena aproximación, intentando encontrar un valor, que denominaremos max(t), tal que se verifique ΔZ(t) < max(t) con probabilidad del 99%.
Si se eligen aleatoriamente N valores de la variable ΔZ(t) se obtendrá una colección de valores...
Reivindicaciones:
1. Método de mantenimiento predictivo de baterías caracterizado porque, utilizando la impedancia de módulo (Z) como variable de diagnosis, comprende los siguientes pasos:
- Realizar mediciones de la impedancia de módulo (Z) sobre los módulos de una batería;
- Definir los valores de aceptación/rechazo (Zcrit) de la impedancia de módulo (Z) para saber si el módulo revisado debe ser intervenido o no;
- Medir durante t meses la impedancia de módulo (Z) para obtener su variación en el tiempo ΔZ(t) y establecer la tendencia en el tiempo de la impedancia de módulo (Z) que permite establecer el periodo de tiempo que tarda un módulo para alcanzar el valor de rechazo (Zcrit).
- Determinar, a partir de la información obtenida de los pasos anteriores, los plazos de mantenimiento que garanticen que la vida útil remanente (L) de la batería es mayor que el periodo de inspección establecido.
2. Método de mantenimiento predictivo de baterías según reivindicación primera, caracterizado porque la fijación de un valor crítico (Zcrit) por debajo del cual se puede garantizar el funcionamiento óptimo de la batería de impedancia Z durante un tiempo t comprende el cálculo de:
en donde:
- ΔZ(t) es la variación de impedancia que experimenta una batería en el plazo de t meses; y
- ΔZmax(t) es el valor supremo de todos los posibles valores de ΔZ(t); es decir: ΔZmax(t) = sup[ΔZ(t)]
3. Método de mantenimiento predictivo de baterías según reivindicación 2, caracterizado porque el cálculo de ΔZmax(t) se obtiene calculando un valor aproximado de ΔZmax(t) denominado max(t), tal que se verifique ΔZ(t) < max(t) con una determinada probabilidad X%.
4. Método de mantenimiento predictivo de baterías según reivindicación 3, caracterizado porque comprende los pasos de:
- Obtención de la función S(N) como:

en donde la colección de valores ΔZ(t)1, ΔZ(t)2, ΔZ(t)3, ..., ΔZ(t)N se obtienen de elegir aleatoriamente N valores a partir de la distribución estadística de la variable ΔZ(t).
- Establecimiento como hipótesis de que, para una determinada batería, ΔZ(t) es independiente de su estado;
- Simulación mediante un método matemático de cuál es el comportamiento de la variable SN definida anteriormente en un número lo suficientemente grande de experimentos;
- Ajuste de la distribución de los sucesivos resultados de todos y cada uno de dichos experimentos de acuerdo a una distribución normal;
- Una vez caracterizada la distribución de SN, se buscará un valor tal que el X% de los valores, sea inferior al que se ha obtenido, obteniéndose como resultado el valor del parámetro max(t) buscado.
Patentes similares o relacionadas:
 DISPOSITIVO DE SUPERVISION Y PROCEDIMIENTO PARA LA DETERMINACION DEL ESTADO DE FUNCIONAMIENTO DE UNA BATERIA DE ACUMULACION, del 5 de Agosto de 2010, de VB AUTOBATTERIE GMBH: Procedimiento para la determinación de la cantidad de energía (QR) que se puede extraer de una batería de acumulación con las etapas:
- […]
DISPOSITIVO DE SUPERVISION Y PROCEDIMIENTO PARA LA DETERMINACION DEL ESTADO DE FUNCIONAMIENTO DE UNA BATERIA DE ACUMULACION, del 5 de Agosto de 2010, de VB AUTOBATTERIE GMBH: Procedimiento para la determinación de la cantidad de energía (QR) que se puede extraer de una batería de acumulación con las etapas:
- […]
 Unidad de suministro de energía eléctrica y control correspondiente, del 27 de Mayo de 2020, de Power-Blox AG: Control para una unidad de suministro de energía eléctrica , que comprende:
a) una primera entrada del nivel de llenado a la cual se puede traspasar […]
Unidad de suministro de energía eléctrica y control correspondiente, del 27 de Mayo de 2020, de Power-Blox AG: Control para una unidad de suministro de energía eléctrica , que comprende:
a) una primera entrada del nivel de llenado a la cual se puede traspasar […]
Circuito de muestreo de alto voltaje de la batería y sistema de gestión de batería, del 13 de Mayo de 2020, de Contemporary Amperex Technology Co., Limited: Un circuito de muestreo de alto voltaje de batería que comprende un relé positivo (G1), un relé negativo (G2), una primera unidad de muestreo positivo (F1), […]
Procedimiento de estimación del estado en que se encuentra una batería, del 11 de Marzo de 2020, de COMMISSARIAT A L'ENERGIE ATOMIQUE ET AUX ENERGIES ALTERNATIVES: Procedimiento de estimación del estado en que se encuentra (SOH) una batería, caracterizado por que comprende las fases siguientes: - Primera fase de […]
Procedimiento de estimación del estado de salud de una batería, del 11 de Marzo de 2020, de COMMISSARIAT A L'ENERGIE ATOMIQUE ET AUX ENERGIES ALTERNATIVES: Procedimiento de estimación del estado de salud SOH de una batería, caracterizado por que comprende las siguientes etapas: • Mediciones (E1) de varios valores […]
MÉTODO Y SISTEMA PARA CALCULAR LA ENERGÍA DISPONIBLE EN UNA BATERÍA ELÉCTRICA EN CUALQUIER MOMENTO DE SU VIDA. SIN DESCARGARLA, ASÍ COMO SU AUTONOMÍA, CAPACIDAD. Y VIDA REMANENTE, del 31 de Enero de 2020, de PARRES GARCÍA, Luis Arturo: Este método calcula la energía disponible, ED, de cualquier batería W, sin descargarla, a cualquier temperatura Tn y en todo momento. Se genera […]
Procedimiento y aparato para mostrar el estado de carga de una batería de un terminal portátil, del 8 de Enero de 2020, de SAMSUNG ELECTRONICS CO., LTD.: Un procedimiento para mostrar la etapa de carga de la batería de un terminal portátil, que comprende: medir una tensión cargada de una unidad de batería […]
Procedimiento de carga, adaptador, terminal móvil y sistema de carga, del 8 de Enero de 2020, de Guangdong OPPO Mobile Telecommunications Corp., Ltd: Un procedimiento de carga para controlar un adaptador de alimentación eléctrica para cargar una batería de un terminal móvil, comprendiendo el procedimiento: comunicarse (S140), […]